Question 824327: Find a polynomial f(x) of degree 3 with real coefficients and the following zeros.
-2, 2 - i
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! A polynomial of degree 3 should have 3 zeros. But only two have been given. The third zero must be found in order to find the polynomial.
The key to finding the third zero is: If a polynomial with real coefficients has complex zeros, then they will always come in conjugate pairs. Since we were given one complex zero, 2 - i, then the missing zero must be its conjugate: 2 + i.
So the three zeros are -2, 2 - i and 2 + i. And when a number, let's call it "z", is a zero of a polynomial, then (x - z) is a factor of the polynomial. So, in factored form,
Simplifying each factor we get:
All that is left is to multiply this out. (Hint for future problems: Multiply the factors with complex conjugate zeros together first.) Multiplying the last two factors can be done with a clever use of the  . To show you how I will do some grouping within those factors:
Treating the "(x-2)" as the "a" of the pattern and the "i" as the "b", this pattern tells us that multiplying the last two factors will result in  :
We can use another pattern,  to square the (x-2). And  . So we get:
which simplifies as follows:
Last we multiply the remaining factors (which I will leave to you). Just multiply each term of (x+2) times each term of 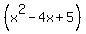 . (That's 6 multiplications!) Then add any like terms. Then put the terms in standard (highest exponent to lowest exponent) order.
|
|
|
