SOLUTION: How do i solve the following equation? A company producing steel construction bars uses the function R(x) = -0.04x2+6.8x -100 to model the unit revenue in dollars for producing x b

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: How do i solve the following equation? A company producing steel construction bars uses the function R(x) = -0.04x2+6.8x -100 to model the unit revenue in dollars for producing x b      Log On


   

Question 824302: How do i solve the following equation? A company producing steel construction bars uses the function R(x) = -0.04x2+6.8x -100 to model the unit revenue in dollars for producing x bars. For what number of bars is the revenue at a maximum? What is the unit revenue at that level of production?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
Take the derivative and set it = to 0 to find the max.


Derivative of 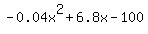+-0.04x%5E2%2B6.8x+-100 = -.08x + 6.8 = 0


-.08x = -6.8


x = 85


Verify it's a max by looking at the value of the derivative for the interval -inf to 85 and 85 to inf. If 85 is a max, the derivative will be positive before 85 and negative after 85.


0 is in the first interval: -.08*0 + 6.8 is positive.


100 is in the second interval: -.08*100 + 6.8 = -8 + 6.8 is negative.


The graph is rising before x=85 and falling after x=85, so 85 is a maximum.
Plug 85 into the equation to find the unit revenue.


+-0.04%2A%2885%5E2%29%2B6.8%2885%29+-100+=+189