Question 824296: What is the distance between the points (2, -4) and (-3, 5)?
Found 2 solutions by jim_thompson5910, josmiceli:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (2, -4), we can say (x1, y1) = (2, -4)
So  , , 
Since the second point is (-3, 5), we can also say (x2, y2) = (-3, 5)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (2, -4) and (-3, 5)

 Plug in Plug in  , ,  , ,  , and , and 





==========================================================
Answer:
The distance between the two points (2, -4) and (-3, 5) is exactly 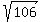 units units
The approximate distance between the two points is about 10.295630140987 units
So again,
Exact Distance: 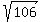 units units
Approximate Distance: 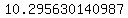 units units
|
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|