SOLUTION: I need more detail solution: Evaluate A = (a^2 − 3a +1)^2 − (1− a)(−2a +1)(1− 3a)

Algebra ->  Customizable Word Problem Solvers  -> Evaluation -> SOLUTION: I need more detail solution: Evaluate A = (a^2 − 3a +1)^2 − (1− a)(−2a +1)(1− 3a)       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 823878: I need more detail solution:
Evaluate A = (a^2 − 3a +1)^2 − (1− a)(−2a +1)(1− 3a)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A way I think is easier:
A=%28a%5E2-3a%2B1%29%5E2-%281-a%29%281-2a%29%281-3a%29
A=%28a%5E2%2B%281-3a%29%29%5E2-%281-3a%2B2a%5E2%29%281-3a%29
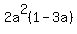A=a%5E4%2B2a%5E2%281-3a%29%2B%281-3a%29%5E2-%281-3a%2B2a%5E2%29%281-3a%29
Taking %281-3a%29 out as a common factor from 2a%5E2%281-3a%29 and %281-3a%29%5E2 we get
A=a%5E4%2B%281-3a%29%282a%5E2%2B1-3a%29%5E2-%281-3a%2B2a%5E2%29%281-3a%29
Notice that the second term, 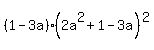%281-3a%29%282a%5E2%2B1-3a%29%5E2 ,
and the third term, 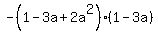-%281-3a%2B2a%5E2%29%281-3a%29 ,
are opposites and cancel each other out.
So we are left with
A=a%5E4

The clench your teeth and dive in way:
A=%28a%5E2-3a%2B1%29%5E2-%281-a%29%281-2a%29%281-3a%29
A=a%5E4-6a%5E3%2B11a%5E2-6a%2B1-%281-3a%2B2a%5E2%29%281-3a%29
A=a%5E4-6a%5E3%2B11a%5E2-6a%2B1-%281-6a%2B11a%5E2-6a%5E2%29
A=a%5E4%2B%28-6a%5E3%2B11a%5E2-6a%2B1%29-%281-6a%2B11a%5E2-6a%5E2%29
Since the two expressions in brackets are the same, they cancel out, and we are left with
A=a%5E4

TIP:
To calculate products like
%28a%5E2-3a%2B1%29%5E2=%28a%5E2-3a%2B1%29%28a%5E2-3a%2B1%29=a%5E4-6a%5E3%2B11a%5E2-6a%2B1 ,
it is better to calculate with pen and paper
by multiplying each term of a%5E2-3a%2B1 times a%5E2-3a%2B1 ,
writing each product in a row,
lining up like terms from the different products,
and then adding up the lines, like this:

------------------------------
matrix%281%2C7%2Ca%5E4%2C-6a%5E3%2C%22%2B%22%2Ca%5E2%2C-61%2C%22%2B%22%2C1%29 matrix%281%2C2%2C%22=%22%2C%28a%5E2-3a%2B1%29%28a%5E2-3a%2B1%29%29
I do it that way, writing only the parts on the left, before the = sign (the rest I only wrote it here to describe how I calculated each line).
Trying to write the calculations on one line, I would get confused and make a mistake.