SOLUTION: Pipe A can fill a tank in 6 hours, and pipe B can fill it in 2 hours less time than it takes drainpipe C to empty the tank. With all three pipes open, it takes 3 hours and 20 minut

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: Pipe A can fill a tank in 6 hours, and pipe B can fill it in 2 hours less time than it takes drainpipe C to empty the tank. With all three pipes open, it takes 3 hours and 20 minut      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 823811: Pipe A can fill a tank in 6 hours, and pipe B can fill it in 2 hours less time than it takes drainpipe C to empty the tank. With all three pipes open, it takes 3 hours and 20 minutes to fill the tank. How long does it take drainpipe C to empty the full tank with pipes A and B closed.
Found 3 solutions by richwmiller, Edwin McCravy, AnlytcPhil:
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
1/6+1/(c-2)-1/c=3/10
c=5
check
1/6+1/3-1/5=3/10
5/30+10/30-6/30=9/30
15-6/30=9/30
ok
or
10/3/6+10/3/(c-2)-10/3/c=1
-10/(3 c)+10/(3 (c-2))+5/9 = 1



Answer by Edwin McCravy(20054) About Me  (Show Source):
Answer by AnlytcPhil(1806) About Me  (Show Source):
You can put this solution on YOUR website!
This is the correct complete solution:

Pipe A can fill a tank in 6 hours,
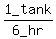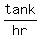
So Pipe A's tank filling rate is 1 tank per 6 hr or 1_tank%2F6_hr or 1%2F6tank%2Fhr

pipe B can fill it in 2 hours less time than it takes drainpipe C to empty the tank (with pipes A and B closed).
 
Suppose drainpipe C can drain 1 tank in x hours.  Then drainpipe C's "filling"
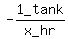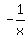
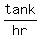
rate is a negative quantity -1 tank per x hours or -1_tank%2Fx_hr or -1%2Fxtank%2Fhr
pipe B can fill it in 2 hours less time than it takes drainpipe C to empty the tank.
 
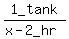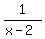
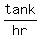
So Pipe B's tank filling rate is 1 tank per x-2 hr or 1_tank%2F%28x-2_hr%29 or 1%2F%28x-2%29tank%2Fhr
With all three pipes open, it takes 3 hours and 20 minutes to fill the tank.
3 hours and 20 minutes is 3%261%2F3 or 10%2F3 hours.  

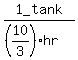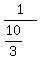
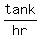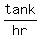So A, B, and C's combined filling rate is 1 tank per 10%2F3 hr or 1_tank%2F%28%2810%2F3%29hr%29 or 1%2F%2810%2F3%29tank%2Fhr or 3%2F10tank%2Fhr

So we have this equation:

%28matrix%284%2C1%2CPipe%2C%22A%27s%22%2Cfilling%2Crate%29%29%22%22%2B%22%22%28matrix%284%2C1%2CPipe%2C%22B%27s%22%2Cfilling%2Crate%29%29%22%22%2B%22%22%22%22=%22%22%28matrix%284%2C1%2CTheir%2Ccombine%2Cfilling%2Crate%29%29

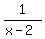
   1%2F6%22%22%2B%22%221%2F%28x-2%29%22%22%2B%22%22-1%2Fx%22%22=%22%223%2F10

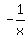
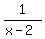
   1%2F6%22%22%2B%22%221%2F%28x-2%29%22%22-%22%221%2Fx%22%22=%22%223%2F10
Multiply through by LCD = 30x(x-2)

   5x(x-2) + 30x - 30(x-2) = 3·3x(x-2)
5x² - 10x + 30x - 30x + 60 = 9x(x-2)
            5x² - 10x + 60 = 9x² - 18x
                         0 = 4x² - 8x - 60

Divide through by 4      0 = x² - 2x - 15
                         0 = (x - 5)(x + 3)
                             x-5=0;   x+3=0
                               x=5;     x=-3 (ignore)

Aswer: 5 hours

Edwin