I need detail solution of this question:
The first term of an arithmetic progression is 8.
a1=8
The sum of the first 10 terms of this progression...
Sn =  [2a1 + (n-1)d]
S10 =
[2a1 + (n-1)d]
S10 =  [2(8) + (10-1)d] =
5[16 + 9d] =
80 + 45d
[2(8) + (10-1)d] =
5[16 + 9d] =
80 + 45d
...divided by...
...the sum of the first 5 terms...
Sn =  [2a1 + (n-1)d]
S5 =
[2a1 + (n-1)d]
S5 =  [2(8) + (5-1)d] =
[2(8) + (5-1)d] =
 [16 + 4d] =
40 + 10d
[16 + 4d] =
40 + 10d
...is 3.25:
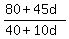 = 3.25 [Note: 3.25=
= 3.25 [Note: 3.25= =
= ]
]
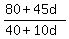 =
=  Cross-multiply:
4(80 + 45d) = 13(40 + 10d)
320 + 180d = 520 + 130d
50d = 200
d = 4
Cross-multiply:
4(80 + 45d) = 13(40 + 10d)
320 + 180d = 520 + 130d
50d = 200
d = 4
How many terms of this progression add up to 1620?
Sn =  [2a1 + (n-1)d]
1620 =
[2a1 + (n-1)d]
1620 =  [2(8) + (n-1)4]
1620 =
[2(8) + (n-1)4]
1620 =  [16 + 4(n-1)]
11620 =
[16 + 4(n-1)]
11620 =  [16 + 4n - 4]
1620 =
[16 + 4n - 4]
1620 =  [12 + 4n]
1620 = 6n + 2nē
0 = 2nē + 6n - 1620
Divide every term by 2
0 = nē + 3n - 810
0 = (n-27)(n+30)
n-27=0; n+30=0
n=27; n=-30 (ignore)
Answer: 27 terms add up to 1620.
Edwin
[12 + 4n]
1620 = 6n + 2nē
0 = 2nē + 6n - 1620
Divide every term by 2
0 = nē + 3n - 810
0 = (n-27)(n+30)
n-27=0; n+30=0
n=27; n=-30 (ignore)
Answer: 27 terms add up to 1620.
Edwin