SOLUTION: So my teacher has asked us to create an equation for a "roller coaster" that has the following requirements: -Your coaster ride must have at least 3 relative maxima and/or minima

Algebra ->  Rational-functions -> SOLUTION: So my teacher has asked us to create an equation for a "roller coaster" that has the following requirements: -Your coaster ride must have at least 3 relative maxima and/or minima       Log On


   

Question 823614: So my teacher has asked us to create an equation for a "roller coaster" that has the following requirements:
-Your coaster ride must have at least 3 relative maxima and/or minima
-the ride length must be at least 4 minutes
-the coaster ride starts at 250 feet
The ride dives below the ground into a tunnel at least once
Any help would be greatly appreciated. I am so lost and it is due tomorrow. Thanks!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A ride longer than 3 minutes would be unusual, but this is not real life roller coaster design.
The simplest answer would be a polynomial function h%28t%29 expressing height (in feet) as a function of time in minutes. Polynomials can have as many turns (maxima and minima) as 1 less than their degree, so a polynomial of degree 4 can have h%280%29=250 , along with 2 minima and one maximum in the (0,ride time) interval, with ridetime%3E=4.
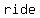A polynomial of higher degree may work nicely too.
A graphing calculator, or graphing software would allow testing different roller coaster designs, until a nice one is found.
The domain of the function must be specified as 0%3C=t%3C=k , where k%3E=4 is the total ride time.
Ground level would be h=0 .
Going before ground level once, the coaster should pass by ground level twice: on the way down and again on the way up. That means two real zeros for the polynomial.

WITHOUT A GRAPHING CALCULATOR:
I would try to make a degree 4 polynomial by multiplying two quadratic polynomials.
Q%28t%29=250%28t-1%29%5E2 is a quadratic with a minimum, Q%28t%29=0 , at t=1 .
It downhill fast at t=0 .
A factor like that may be a good start for the ride.
We could also use any other quadratic equation. They all have one maximum (or one minimum, if the leading coefficient is negative.
The function h%28t%29 could dip below ground at t=2 and come back up at t=4 . We can accomplish that by having
P%28t%29=%28t-2%29%28t-4%29 as a factor.

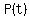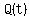The product of the P%28t%29 and Q%28t%29 would be a polynomial of degree 4 that would have two minima and one maxima between t=0 and t=5 .

There are many 4th degree polynomials with a positive leading coefficient that would work. You need to make sure that they have two zeros in the (0,end of domain) interval (end of domain>=4), that there are 2 maxima in that interval, and that there is a negative minimum.
It would also be nice if h%28t%29 did not take any unreasonable values in the (0,ride time) interval, because real roller coaster do not get much taller than 400 feet, and we do not want that tunnel to be too deep either.
ON second thought, it would also be more realistic if the roller coaster never got as high as 250 feet again, because what moves is only gravity.

h%5B1%5D%28t%29=%285%2F3%29%28t-5%29%5E2%28t-2%29%28t-3%29 , with ridetime%3E5 ,
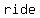would work, because the second minimum happens at t=5 .
graph%28300%2C300%2C-1%2C6%2C-30%2C270%2C%285%2F3%29%28x-5%29%5E2%28x-2%29%28x-3%29%29

That ride does not look like much fun, and with a degree 4 polynomial, the riders would be getting off at a point where the track is uphill.

WITH A GRAPHING CALCULATOR OR SOFTWARE:
With some help for graphing, we could have a better design.
Maybe we should aim for a degree 5 polynomial and let the riders out at the next maximum.
Something based on p%28t%29=-%28t-1%29%28t-2%29%28t-3%29%28t-4%29%28t-5%29 sounds like it could work.
p%280%29=2%2A3%2A4%2A5=120 and it goes below zero between 1 and 2 and between 3 and 4.
Multiplied times 250%2F120=25%2F12 it would have p%280%29=250 .

However, it does not dip too far below zero, and it does not rise too high during the ride. It would not be fun. Besides, the coaster would go below ground twice, and maybe the problem meant to say "just once".
q%28t%29=-%28t-0.5%29%28t-1%29%28t-3%29%28t-4%29%28t-5%29 , with q%280%29=0.5%2A3%2A4%2A5=30 , looks better.
Because the first 2 zeros are close together, the first dip does not go too low.
Adding 2, that first dip does not go below zero, and the value for t=0 is 32.
Next, multiplying times 250%2F32=125%2F16 we get
h%5B2%5D%28t%29=%28125%2F16%29%282-%28t-0.5%29%28t-1%29%28t-3%29%28t-4%29%28t-5%29%29 , or
h%5B2%5D%28t%29=125%2F8-%28125%2F16%29%28t-0.5%29%28t-1%29%28t-3%29%28t-4%29%28t-5%29
with h%5B2%5D%280%29=250 , 2 minima and 2 maxima.
That second maximum could be the end of the ride.

However, the lowest minimum would have h%5B2%5D%280%29=about6.4feet and that is not a reasonable depth for a tunnel.

An improved version , q%5B2%5D%28t%29=-%28t-0.5%29%28t-1%29%28t-4%29%28t-6%29%28t-7%29 , with q%280%29=0.5%2A4%2A6%2A7=84 , looks better.
Adding 12, the first dip does not go below zero, and the value for t=0 is 100.
Next, multiplying times 250%2F100=2.5 we get
h%5B2%5D%28t%29=2.5%282-%28t-0.5%29%28t-1%29%28t-4%29%28t-6%29%28t-7%29%29 , or
h%5B2%5D%28t%29=40-2.5%28t-0.5%29%28t-1%29%28t-4%29%28t-6%29%28t-7%29
with h%5B2%5D%280%29=250 , 2 minima and 2 maxima.
That second maximum could be the end of the ride.