|
Question 823594: Hello, I have a problem, that I dont know what am I doing wrong with it.The problem is like this:
A vendor sends an invoice that totals $6115.68, this invoice contains 2 types of products that have different prices.
Product 1: $1.65 per case
Product 2: $2.46 per case.
How many cases of each product is the vendor charging for?
I just cant figure out how to do this, can someone please explain me?
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = number of cases of product 1. = number of cases of product 1.
 = number of cases of product 2. = number of cases of product 2.
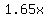 = cost in $ for = cost in $ for  units of product 1. units of product 1.
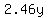 = cost in $ for = cost in $ for  units of product 2. units of product 2.
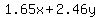 = total cost for = total cost for  units of product 1, and units of product 1, and  units of product 2. units of product 2.
according to the vendor's invoice, that is $6115.68, so
 is our equation. is our equation.
We have two variables and only one equation.
In general that would mean an infinite number of answers.
However, in this case, only integer, non-negative solutions would work.
That limits the number of solutions.



Once we find one solution, we can increase the  found by found by 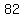 while decreasing the while decreasing the  found by found by  . .
That would change both terms by  units and in opposite directions, so that they would still add up to units and in opposite directions, so that they would still add up to 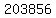 . .
Since 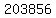 divided by divided by 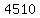 yields a quotient of yields a quotient of  with a remainder of with a remainder of 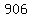 , there are at least , there are at least  solutions, and maybe solutions, and maybe 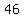 . .
If  , ,  transforms into transforms into
 , ,  , and , and  . .
So one of the possible solutions is  . .
That is a non-negative integer, so it is allowed to be  and and  . .
That solution means 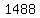 units of each product. units of each product.
It could be that there were 55 less units of product 2,
meaning  units of product 2, units of product 2,
but 82 more units of product 1,
meaning  . .
That would decrease the term 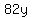 by by  , ,
but would increase term 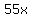 by by  . .
The total would still be 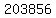 , with , with  and and  . .
We could repeat the procedure a few more times, as long as the decreasing  is still a nonn-egative number. is still a nonn-egative number.
Since 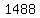 divided by divided by  has a quotient of has a quotient of  with a remainder of with a remainder of  , we can do that decreasing , we can do that decreasing  by by  a total of a total of  times until we get to times until we get to  . .
That means that besides ordered pair (x,y)=(1488,1488), There are  other solutions with lesser values of other solutions with lesser values of  , going all the way to , going all the way to  , ,  . .
On the other hand, we could decrease  by 82, while increasing by 82, while increasing  by 55. by 55.
That would give us another  solutions, with solutions, with  decreasing all the way to decreasing all the way to  because because 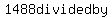 yields a quotient of yields a quotient of  and a remainder of 12. and a remainder of 12.
There is a total of  solutions: solutions:
 units of product 1 with units of product 1 with 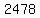 units of product 2, units of product 2,
 units of product 1 with units of product 1 with  units of product 2, units of product 2,
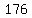 units of product 1 with units of product 1 with 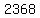 units of product 2, units of product 2,
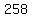 units of product 1 with units of product 1 with 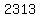 units of product 2, units of product 2,
and so on, all the way to
 units of product 1 with units of product 1 with  units of product 2. units of product 2.
I guess we could write them as
 paired with paired with 
foe  integer, such that integer, such that 
|
|
|
| |