SOLUTION: In the formula N = Pekt, N is the number of items in terms of an initial population P at a given time t and k is a growth constant equal to the percent of growth per unit time. How

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: In the formula N = Pekt, N is the number of items in terms of an initial population P at a given time t and k is a growth constant equal to the percent of growth per unit time. How      Log On


   

Question 823566: In the formula N = Pekt, N is the number of items in terms of an initial population P at a given time t and k is a growth constant equal to the percent of growth per unit time. How long will it take for the population of a certain country to double if its annual growth rate is 3.2%? Round to the nearest year
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Please use "^" to indicate exponents and please put exponents which are not just a positive number or variable in parentheses. You should post:
N = Pe^(kt)

With the given growth rate, this equation is:
N+=+Pe%5E%280.032t%29
(Note that the percentage was changed to an equivalent decimal. Percents as percents should not be used in formulas/calculations!)

If P is the initial population then the population will have doubled if it reaches 2P. So we replace the N with 2P and solve:
2P+=+Pe%5E%280.032t%29
First we isolate the base, e, and its exponent. Dividing both sides by P:
2+=+e%5E%280.032t%29
Next, with the variable in the exponent, we use logarithms. Any base of logarithm may be used. But there are advantages to choosing certain bases:
  • Choosing a base for the logarithm that matches the base of the exponent will result in the simplest possible expression for the solution.
  • Choosing a base for the logarithm which your calculator "knows", base 10 ("log") or base e ("ln"), will result in an expression which can easily be converted to a decimal approximation.
By choosing base e logs, "ln", we can get both advantages:
ln%282%29+=+ln%28e%5E%280.032t%29%29

Next we use a property of logarithms, log%28a%2C+%28p%5En%29%29+=+n%2Alog%28a%2C+%28p%29%29, which allows us to move the exponent in the argument out in front. (It is this property which is the reason for using logs in the first place. It allows us to move the exponent, where the variable is, out in front where we can "get at" the variable and solve for it.)
ln%282%29+=+%280.032t%29ln%28e%29

By definition ln(e) = 1. (This is why matching the bases of the log and the exponent leads to simpler expressions.)
ln%282%29+=+0.032t

Now we just divide by 0.032:
ln%282%29%2F0.032+=+t
This is an exact expression for the solution. But since saying "It will take 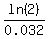ln%282%29%2F0.032 years for the population to double." is awkward, we will use our calculator to get a decimal approximation:
0.6931%2F0.032+=+t (The log has been rounded to 4 places.)
21.6594+=+t
Now we can say: It will take approximately 21.7 years for the population to double.