Question 823339: Find the set of polygons in which the number of diagonals is greater than the sum of the measures of the angles. Please help me figure this out. I've tried everything.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume it is the sum of the measures of the interior angles, in degrees.
If you measure the angles in radians, there is no solution.
The number of diagonals in a polygon with  sides is sides is
 . .
The sum of the interior angles, in degrees, is
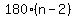 . .
The inequality to solve is
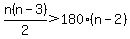
Solving:
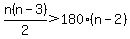

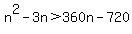


 is a quadratic function. is a quadratic function.
It graphs as a parabola with a minimum.
It may be negative for a certain interval of intermediate values,
but outside of that middle interval it will be positive, so we will have some solutions.
We know that  , ,
but we want to know the solutions for  , ,
because a polygon has to have at least 3 sides.
If we find the solutions to  , if any, , if any,
those solutions will be the ends of that middle interval where 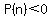 and and
we will have our answer.
Applying the quadratic formula to  we find we find
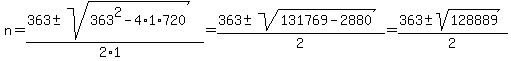
The approximate values are
 and and 
For the number of diagonals to be greater than the sum of the measures of the interior angles in degrees, we need
either 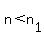 , ,
or 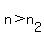 . .
The inequality 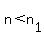 gives no polygon solution. gives no polygon solution.
The inequality 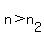 means that all polygons with means that all polygons with  (362 or more sides) will have (362 or more sides) will have
a number of diagonals that is greater than the sum of the measures of the interior angles in degrees.
|
|
|