SOLUTION: Find the half-life of a radioactive substance if 240 grams of the substance decays to 180 grams in 9 years. Use Q(t)=e^kt, just not sure how to get the answer!

You don't have the formula correct.  The formula must have 
Q(0) before the ekt.  The correct formula is

Q(t)=Q(0)ekt

That says Q(0)=240 and Q(9)=180 (that's when t=9).
Plug those in to

Q(t) = Q(0)ekt
Q(9) = 240ek·9
 180 = 240e9k

Divide both sides by 240
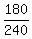  = e9k
 0.75 = e9k

Use the principle that exponential equation A=eB is equivalent 
to natural logarithm equation B=lnA:

9k = ln(0.75)
 k = ln(0.75)/9
Use calculator:
 k = -0.0319646747

So the formula 

Q(t) = Q(0)ekt

now becomes

Q(t) = Q(0)e-0.0319646747t

Now to find the half life.  That will be when any original quantity
reduces to one-half of its original quantity.  It's how long it takes 
240 grams to decay to 120 grams, or for 100 grams to decay to 50 grams 
or for any number of grams to decay to one-half of that number of grams.

In general, it's when the original quantity Q(0) decays to Q(0).

So we substitute Q(0) for Q(t) and solve for t

Q(t) = Q(0)e-0.0319646747t
Q(0) = Q(0)e-0.0319646747t

Divide both sides by Q(0)

 = e-0.0319646747t     

Use the principle that exponential equation A=eB is equivalent 
to natural logarithm equation B=lnA:

-0.0319646747t =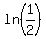 
-0.0319646747t = ln(0.5)
Use calculator
-0.0319646747t = -0.6931471806
             t = 
             t = 21.68478757 years

Edwin