Question 822959: The equation of an ellipse with center (5,3) that passes through the points (9,3) and (5,5) has the form f(x,y)=1. Find f(x,0).
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem is not very difficult once you recognize that the two points, (9, 3) and (5, 5), are not just any two points on the ellipse. Since (9, 3) has the same y-coordinate as the center it is a vertex on the horizontal axis. And since (5, 5) has the same x-coordinate as the center, it is a vertex on the vertical axis.
Since the distance from (9, 3) to the center is 6 and the distance from (5, 5) to the center is 2: a = 6, b = 2 and the ellipse is horizontal. With a center of (5, 3), the equation for the ellipse is:

The left side the the f(x, y) mentioned in the problem. To find f(x, 0) we just replace the "y" with zero in f(x, y):
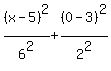
Now we simplify:
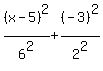

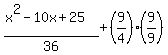

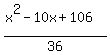
This is f(x, 0).
|
|
|