Question 822729: Figure 1 represents a conical container with a diameter of 120cm and a depth of 140cm. It is filled with water to a depth of 60cm.
a) Find the volume of water in the container. (SOLVED)
b) Find the surface area of container in contact with the water. (SOLVED)
c)The container in Fig. 1 is inverted so that the water is now at the base of the cone with height h cm. Calculate the value of h.
* Fig. 1's cone is inverted with the tip facing down , fig
2's cone is the upright one with th base on the ground.
Appreciate your help as this is the last question for my holiday assignment. Thanks !
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The volume of a cone can be calculated as 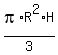 , ,
where  is the radius of the base and is the radius of the base and 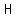 is the height of the cone. is the height of the cone.
Inside that conical container,
there is a cone of water at first,
with air above it.
When the container is inverted,
there is a cone of air on top,
and water below it.
All the cones are similar.
The radius of the conical container,  is is
 of the height. of the height.
 <---> <---> 
The ratio is the same for all the other similar cones.
Their volume is

The volume of the conical container, in cubic centimeters, is
 . .
The volume of water in the container, in cubic centimeters, is
 . .
The volume of air in the container, in cubic centimeters, is
 . .
We can find the height, 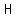 , of the cone of air, in cm: , of the cone of air, in cm:





Once the cone is standing on its base, there is a cone of air inside the tip of the container that has a height of 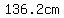 . .
If 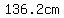 at the tip of the cone are air, the remaining at the tip of the cone are air, the remaining  at the base of the cone are full of water. at the base of the cone are full of water.

|
|
|