Question 822676: if four of the angles of the pentagon are x,2x,3x,4x.
two opposite sides are parallel, how to find the value of x...??
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! if four of the angles of the pentagon are x,2x,3x,4x.
two opposite sides are parallel, how to find the value of x...??
Since you didn't specify which two opposite sides are parallel,
there are four solutions for x. Only one of them, the first, x=40°
defines a convex pentagon. The other three are concave polygons. A
concave polygon has one or more "sunk-in places" where one or more
of the internal angles are greater than 180°, and are called REFLEX
angles. Examples of pentagons defined by the four solutions are all
drawn below.
Since two sides are parallel, one of the sides must be a transversal
between those two parallel sides. This means that two of the interior
angles are supplementary.
The sum of the interior angles of a pentagon are
(n-2)×180° = (5-2)×180° = 3×180° = 540°
Let the 5th interior angle be y, then
x+2x+3x+4x+y = 540°
10x+y = 540°
y = 540°-10x
So the 5 angles are
x, 2x, 3x, 4x, 540°-10x
There are 9 cases for the 2 supplementary angles:
Case 1: x and 2x are supplementary:
x+2x=180° or 3x=180° or x=60°, so the 5 angles would be
60°, 120°, 180°, 240°, -60° not possible
Case 2: x and 3x are supplementary:
x+3x=180° or 4x=180° or x=45°, so the 5 angles would be
45°, 90°, 135°, 180°, 90°, not possible because an
interior angle cannot be 180°, for that would have only
4 sides.
Case 3: x and 4x are supplementary:
x+4x=180° or 5x=180° or x=36°, so the 5 angles would be
36°, 72°, 108°, 144°, 180°, not possible because an interior
angle cannot be 180°, for that would have only 4 sides.
Case 4: x and 540°-10x are supplementary:
x+540°-10x=180° or -9x=-360° or x=40°, so the 5 angles would be
40°, 80°, 120°, 160°, 140°, which IS POSSIBLE!
Case 5: 2x and 3x are supplementary:
x+3x=180° or 4x=180° or x=45°, so the 5 angles would be
45°, 90°, 135°, 180°, 90°, not possible because an interior
angle cannot be 180°, for that would have only 4 sides.
Case 6: 2x and 4x are supplementary:
2x+4x=180° or 6x=180° or x=30°, so the 5 angles would be
30°, 60°, 90°, 120°, 240°, which IS POSSIBLE!
Case 7: 2x and 540°-10x are supplementary:
2x+540°-10x=180° or -8x=-360° or x=45°, same as case 5
Case 8: 3x and 4x are supplementary:
3x+4x=180° or 7x=180° or x=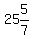 °, so the 5 angles would be °, so the 5 angles would be
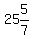 °, °, 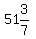 °, °,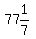 °, °, 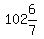 °, °, 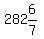 °, which IS POSSIBLE!
Case 9: 3x and 540°-10x are supplementary:
3x+540°-10x=180° or -7x=-360° or x= °, which IS POSSIBLE!
Case 9: 3x and 540°-10x are supplementary:
3x+540°-10x=180° or -7x=-360° or x=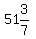 °, so the 5 angles
would be °, so the 5 angles
would be 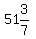 °, °, 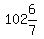 °, °, 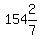 °, °, 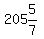 , ,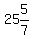 °
which IS POSSIBLE!
Case 10: 4x and 540°-10x are supplementary:
4x+540°-10x=180° or -6x=-360° or x=60°, same as case 1. NOT
POSSIBLE!
So there are four solutions for x:
1. x=40°, 2x=80°, 3x=120°, 4x=160°, 5th angle=140°
2. x=30°, 2x=60°, 3x=90°, 4x=120°, 5th angle=240°
3. x= °
which IS POSSIBLE!
Case 10: 4x and 540°-10x are supplementary:
4x+540°-10x=180° or -6x=-360° or x=60°, same as case 1. NOT
POSSIBLE!
So there are four solutions for x:
1. x=40°, 2x=80°, 3x=120°, 4x=160°, 5th angle=140°
2. x=30°, 2x=60°, 3x=90°, 4x=120°, 5th angle=240°
3. x=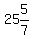 °, 2x= °, 2x=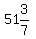 °, 3x= °, 3x=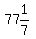 °, 4x= °, 4x=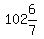 °, 5th angle= °, 5th angle=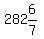 °
4. x= °
4. x=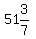 °, 2x= °, 2x=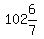 °, 3x= °, 3x=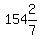 °, 4x= °, 4x=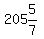 , 5th angle= , 5th angle=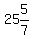 °.
Here are typical ways the 5 pentagons could be. The
internal angles which are more than 180° which cause
the last 3 pentagons to be concave are indicated with
a red arc.
1. 40°, 80°, 120°, 160°, 140° °.
Here are typical ways the 5 pentagons could be. The
internal angles which are more than 180° which cause
the last 3 pentagons to be concave are indicated with
a red arc.
1. 40°, 80°, 120°, 160°, 140°
 2. 30°, 60°, 90°, 120°, 240°,
2. 30°, 60°, 90°, 120°, 240°,
 3.
3. 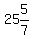 °, °, 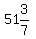 °, °,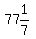 °, °, 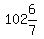 °, °, 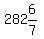 ° °
 4.
4. 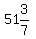 °, °, 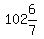 °, °, 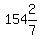 °, °, 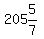 , ,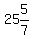 ° °
 Edwin
Edwin
|
|
|