in an arithmetic sequence, the sum of the first 20 terms is 950 and the sum of the second 20 terms is 0. find the general term of the sequence.
Sn =  [2a1 + (n-1)d]
950 =
[2a1 + (n-1)d]
950 = 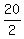 [2a1 + (20-1)d] =
950 = 10[2a1 + 19d] =
Divide through by 10
95 = 2a1 + 19d
[2a1 + (20-1)d] =
950 = 10[2a1 + 19d] =
Divide through by 10
95 = 2a1 + 19d
the sum of the second 20 terms is 0.
That means the sum of the first 40 terms is also 950
Sn =  [2a1 + (n-1)d]
950 =
[2a1 + (n-1)d]
950 = 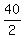 [2a1 + (39)d] =
950 = 20[2a1 + 39d] =
Divide through by 10
95 = 2[2a1 + 39d]
95 = 4a1 + 78d
So we have this system of equations:
95 = 2a1 + 19d
95 = 4a1 + 78d
To eliminate a1, multiply the
first one through by -2
-190 = -4a1 - 38d
95 = 4a1 + 78d
-------------------
-95 = 40d
[2a1 + (39)d] =
950 = 20[2a1 + 39d] =
Divide through by 10
95 = 2[2a1 + 39d]
95 = 4a1 + 78d
So we have this system of equations:
95 = 2a1 + 19d
95 = 4a1 + 78d
To eliminate a1, multiply the
first one through by -2
-190 = -4a1 - 38d
95 = 4a1 + 78d
-------------------
-95 = 40d
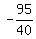 = d
= d
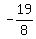 = d
95 = 2a1 + 19d
95 = 4a1 + 78d
To eliminate d, multiply the
first one through by -78, and
the second one through by 19
-7410 = -156a1 - 1482d
1805 = 76a1 + 1482d
-------------------
-5605 = -80a1
= d
95 = 2a1 + 19d
95 = 4a1 + 78d
To eliminate d, multiply the
first one through by -78, and
the second one through by 19
-7410 = -156a1 - 1482d
1805 = 76a1 + 1482d
-------------------
-5605 = -80a1
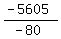 = a1
= a1
 = a1
Use nth term formula:
an = a1 + (n-1)d
an =
= a1
Use nth term formula:
an = a1 + (n-1)d
an =  + (n-1)
+ (n-1)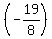 an =
an =  +
+ 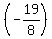 (n-1)
Multiply through by 16
16an = 1121 + (-38)(n-1)
16an = 1121 - 38(n-1)
16an = 1121 - 38n + 1
16an = 1122 - 38n
Divide through by 2
8an = 561 - 19n
an =
(n-1)
Multiply through by 16
16an = 1121 + (-38)(n-1)
16an = 1121 - 38(n-1)
16an = 1121 - 38n + 1
16an = 1122 - 38n
Divide through by 2
8an = 561 - 19n
an =  Edwin
Edwin