Question 822545: what is the 20th term of 16,49,104,181 ?
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
16,49,104,181
I always first check the sequence of differences to see
if I can recognize a pattern:
2nd term - 1st term = 49-16 = 33 = 11×3
3rd term - 2nd term = 104-49 = 55 = 11×5
4th term - 3rd term = 181-104 = 77 = 11×7
So we can now see the pattern.
1. Start with 16, then
2. 16 + 11×3 = 49
and the multiple of 11, which is 3, is 1 less than twice the term
number, which is 2.
3. 49 + 11×5 = 104 =
16 + 11×3 + 11×5
and the multiple of 11, which is 5, is 1 less than twice the term
number, which is 3.
4. 104 + 11×7 = 181 =
16 + 11×3 + 11×5 + 11×7
and the multiple of 11, which is 7, is 1 less than twice the term
number, which is 4
Therefore to find the 20th term, we start with 16 and add
19 terms. So the 20th term is
16+ =
Factor out 11 from the sun:
16+ =
Factor out 11 from the sun:
16+ =
Break up the sum into two sums:
16+ =
Break up the sum into two sums:
16+ =
Factor out 2 from the first sum:
16+ =
Factor out 2 from the first sum:
16+ =
The sum =
The sum  is the sum of an arithmetic sequence
with a1 = 2 and a19 = 20, and d=1
Sn = is the sum of an arithmetic sequence
with a1 = 2 and a19 = 20, and d=1
Sn =  (a1 + an)
S19 = (a1 + an)
S19 = 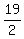 (2 + 20) = (2 + 20) = 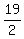 (22) = 209
And (22) = 209
And  is the sum of 19 ones, which is 19.
Substituting in:
16+ is the sum of 19 ones, which is 19.
Substituting in:
16+ =
We have
16+11·(2·209-19) =
4405.
Edwin =
We have
16+11·(2·209-19) =
4405.
Edwin
|
|
|