SOLUTION: What is the standard form and state whether it is a parabola, a circle, an ellipse, or a hyperbla f 3x^2=8-4y^2-8y

First get a 0 on the right side:

                   3x² + 4y² + 8y - 8 = 0  

Rule: If the polynomial equation of degree 2 contains no terms in xy 
and has 0 on the right side, then

 I. If it has only one squared letter, it is a parabola.
    A. If the squared letter is x², the axis of symmetry is vertical
    B. If the squared letter is y², the axis of symmetry is horizontal.
II. If it has two squared letters then
   A. If the coefficients of the squared letters have the same sign
      then it is an ellipse.
      1. If the coefficients of the squared letters are also equal, it is a 
         circle, which is a special kind of ellipse.
      2. If the coefficients of the squared letters are not equal but have the
         same sign, it is an ellipse which is not a circle.
      3. If the coefficient of x² is smaller in absolute value than the
         coefficient of y², then its major axis is horizontal. 
      4. If the coefficient of y² is smaller in absolute value than the
         coefficient of x², then its major axis is vertical. 

   B. If the coefficients of the squared letters have opposite signs, then
      it is a hyperbola.

So
                   3x² + 4y² + 8y - 8 = 0

fits II A 2, so it is an ellipse which is not a circle, and whose
major axis is horizontal since 3 < 4.

To get it in standard form, we have to make it look like this:

                  +  =  
              
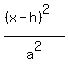Get the constant term on the right:

                      3x² + 4y² + 8y = 8                           

Since there are no terms in x, we complete the square on x simply
by replacing x by (x - 0) 

                3(x - 0)² + 4y² + 8y = 8

To complete the square on the y terma, first factor out the
coefficient of y² out of both the y² and the y terms:

              3(x - 0)² + 4(y² + 2y) = 8

Multiply the coefficient of y, which is 2, by 1/2, getting 1
Then square the 1 getting 1.  Add this inside the parentheses
on the left.  This amounts to adding 4×1 to the left side of
the equation since the parentheses has a 4 multiplied by it.
Therefore to compensate, we must add 4 to the right side:

          3(x - 0)² + 4(y² + 2y + 1) = 8 + 4

Factor the trinomial inside the second parentheses as a
perfect square, combine terms on the right:

               3(x - 0)² + 4(y + 1)² = 12

Get 1 on the right side by dividing every term by 12

             +  =  

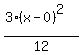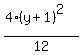Divide top and bottom of the first fraction by 3, top and bottom
of the second fraction by 4 and simplify the right side as just 1:

             +  =  

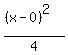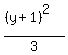That's the standard form., which is all you're looking for. But
you will eventually be asked for more, so here is some more:

Comparing that to:

         +  = 
                           
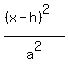h = 0, k = -1, a = 2, b = 

So its center is (h,k) = (0,-1). Its semi-major akis is a = 2, and
its semi-minor axis is b = 

To draw its graph we locate the center, and draw the complete major
axis and minor axes intersecting at the center (0,-1), like this:



Then sketch in the ellipse:

 

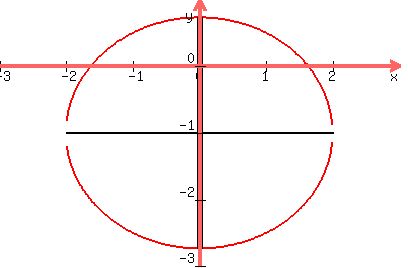It looks almost like a circle, but if you'll look  carefully it's
not really because its a little bit fatter than it is tall.  They 
only begin to look egg-shaped when b is less than half of a.

The two foci (focal points) are on the major axis each a distance
 of c units from the center, where c² = a² - b²

                                   c² = 4 - 3 
                                   c² = 1 
                                    c = 1

So the foci are at (1,1) and (-1,-1) marked below as o's,
1 unit from the center (0,-1)

 

Edwin