SOLUTION: I don't know what kind of problem this is...please help! Sketch a quadratic function with zeros at -3 and 1. I don't understand the "zeros at -3 and 1" part.

Algebra ->  Linear-equations -> SOLUTION: I don't know what kind of problem this is...please help! Sketch a quadratic function with zeros at -3 and 1. I don't understand the "zeros at -3 and 1" part.      Log On


   

Question 821639: I don't know what kind of problem this is...please help!
Sketch a quadratic function with zeros at -3 and 1. I don't understand the "zeros at -3 and 1" part.
Found 2 solutions by josmiceli, KMST:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Zero is just another name for root
You are given:
+x+=+-3+
+x+=+1+
Or, what is the same thing:
+x+%2B+3++=+0+
+x+-+1+=+0+
---------------
Multiplying these:
+%28+x%2B3+%29%2A%28+x-1+%29+=+0+
+x%5E2+%2B+3x+-+x+-+3+=+0+
+x%5E2+%2B+2x+-+3+=+0+
You are asked to sketch the function
+f%28x%29+=+x%5E2+%2B+2x+-+3+
+graph%28+400%2C+400%2C+-6%2C+6%2C+-6%2C+10%2C+x%5E2+%2B+2x+-+3+%29+

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
This problem does not require much work, because there are many correct answers.
You do not need much information or calculations to do that sketch.
You need information to understand the question.
Knowing the meaning of some words used by math teachers helps.
For example a quadratic function is a polynomial function of degree 2, meaning something like
y=3x%5E2%2B5x%2B2 or f%28x%29=x%5E2%2B2x-3 .
The graph of a quadratic function is a curve called a parabola, with a more or less pointy "end" called the vertex of the parabola.
It also helps if you know some tricks old mathematicians used to solve similar problems, but you should understand how they figured it out, or at least why those procedures work.

One of many functions with zeros at -3 and 1 is

It is a quadratic function that
becomes zero when x=1 because the first factor is zero, and
becomes zero when x=-3 because the second factor is zero.
So x=1 and x=-3 are called zeros of the function.
You could write that function in the factored form,
y=%28x-1%29%28x%2B3%29
or in the standard polynomial form,
y=x%5E2%2B2x-3
or in the vertex form,
y=%28x%2B1%29%5E2-4 .
All quadratic functions can be written in the standard form and in the vertex form.
If the zeros are rational numbers, there is also a nice-looking factored form.
In that case, it can be proven that the x at the vertex is the average of the zeros.
So the x at the vertex is x=%281%2B%28-3%29%29%2F2=%28-2%29%2F2=-1 ,
and then y at the vertex can be found by substituting -1 for x in one of the forms of the equation for that function.

There are many other quadratic functions with the same zeros,
because multiplying 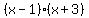%28x-1%29%28x%2B3%29 times some non-zero number does not change where the product is zero.
For example y=2%28x-1%29%28x%2B3%29 is another quadratic function with zeros at -3 and 1. Its graph is graph%28200%2C200%2C-5%2C5%2C-8%2C2%2C2x%5E2%2B4x-6%29
So is y=-1%28x-1%29%28x%2B3%29=-x%5E2-2x%2B3 with the graph graph%28200%2C200%2C-5%2C5%2C-5%2C5%2C-x%5E2-2x%2B3%29
Multiplying times a factor may change the value of y at the vertex, but not the zeros or the x at the vertex.
So any graph that you sketch looking like that (crossing the x-axis at -3 and 1, and symmetrical to both sides of x=-1 may be a good answer.

EXTRA:
The vertex form is the most useful form of the equation if you want to sketch the graph of a particular function,
because it tells you the vertex position.
The minimum value for y=%28x%2B1%29%5E2-red%284%29 is y=-red%284%29 , and happens when x=-1<-->x%2B1=0<-->%28x%2B1%29%5E2=0<-->%28x%2B1%29%5E2-4=-4
For all other values of 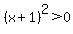x , %28x%2B1%29%5E2%3E0 and y=%28x%2B1%29%5E2-4%3E-4 .
That point, with x=-1 and y=-4 is the vertex of the graph.