Question 821433: Find the exact value of the function
tan(beta/2), given tan(beta)= -((sqrt 5)/2), with 90 degrees < beta < 180 degrees
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!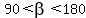 
This tells us that  terminates in the second quadrant, where x-coordinates are negative and y-coordinates are positive.
At this point a diagram may be helpful:- Draw an angle in standard position which terminates in the 2nd quadrant. This angle will be .
- From somewhere on the terminal side draw a perpendicular down to the x-axis. This perpendicular, the x-axis and the terminal side form a right triangle.
- We've been given that
 . Since tan is opposite/adjacent, we want to label the opposite site with the numerator of 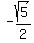 and the adjacent side with the denominator. But where does the "=" go? Answer: Since we are in the 2nd quadrant, the minus should go with the adjacent side (x-axis). So label the opposite side, the perpendicular, as  and label the adjacent side (x-axis) as -2.
For 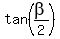 we will use the tan((1/2)x) identity:
From this we can see that we will need  and  . For both sin and cos we need the hypotenuse. So we use the Pythagorean Theorem to find the hypotenuse:
 (where "h" represents the hypotenuse)
Simplifying...
 (ignoring the negative square root of 9 since hypotenuse's are never negative).
Now that we have the hypotenuse, we can find the sin, opposite/hypotenuse, and the cos, adjacent/hypotenuse, of :
And finally we can find :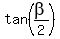
Substituting in the values we found for sin and cos:
Simplifying...
|
|
|
