Question 821307: x^2-3x^5>10
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 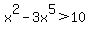
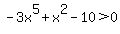
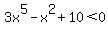
A graphing calculator would tell you that
 happens for happens for  (rounded), (rounded),
with the 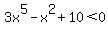 only for only for 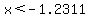 . .
Before graphing calculators, I would have calculated the derivative as
 = =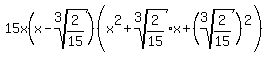
Since the last factor is always positive, the zeros of the derivative are at  and at and at  . .
The derivative is negative in between those two values of  , ,
meaning that is an interval where  decreases. decreases.
For other values of  , the derivative is positive and the function increases. , the derivative is positive and the function increases.
At  where where  we have a maximum of we have a maximum of  , ,
and at  , a minimum of , a minimum of  , where , where 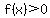 . .
Since  and and  , ,
The value of  that makes that makes  is in between, is in between, 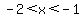 . .
At that point we would try guess-and-check values in between, aiming to get closer limits on  , maybe going through , maybe going through
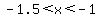 , ,  , , 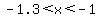 and so on, until I got a close enough approximation. and so on, until I got a close enough approximation.
|
|
|