SOLUTION: Using synthetic division can someone help me determine the quotient to these problems? 1. F(x)=2x³+8x²-5x+5; G(x)=x-2 2. f(x)=x⁴-x²+3x; g(x)=x+1 3. Find the

Synthetic division gives you an easier way to do two 
different things:

A. An easier way to divide a polynomial by a binomial of
the form x±↏, where there is a number in the box. The 
sign can either be + or -.

B. An easier way to substitute a number in a polynomial.


----------------------------------
1. F(x)=2x³+8x²-5x+5; G(x)=x-2

Change the sign of the -2 to +2

2|2  8 -5  5
 |   4 24 38 
  2 12 19 43

The numbers across the bottom all except the last one
tells you the coefficients of the quotient.  The last
number is the remainder.  

The quotient is always one degree less than the original
polynomial.  The original polynomial is degree 3 so
the quotient polynomial will be degree 2

2x²+12x+19 with remainder 43

or you can write it  2x²+12x+19+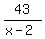 

It is a shortcut for this long division:

         2x²+12x+19      
x-2)2x³+ 8x²- 5x+ 5
    2x³- 4x²
        12x²- 5x
        12x²-24x
             19x+ 5
             19x-38
                 43
----------------------------------

f(x)=x4-x²+3x; g(x)=x+1

This one is like the first one except that you must put in
two zero placeholders

You must consider f(x) as this:

f(x) = x4-0x3-x2+3x+0

and start with this:

-1| 1  0 -1  3  0
  |______________

You finish it.
       
------------------------

f(x)= -15x³+18x²-x+2 at x=-2

This is the other use for synthetic division. A shortcut
for substituting into a polynomial:

Uss the same value -2 (do not change the sign)

-2|-15  18  -1    2
  |     30 -96  194
   -15  48 -97  196

The answer is the remainder 196. (Ignore the other numbers)

That's a shortcut for this substitution for x and simplifying: 

f(x)= -15x³+18x²-x+2 at x=-2

f(-2) = -15(-2)³+18(-2)²-(-2)+2
f(-2) = -15(-8)+36(4)+2+2
f(-2) = 120+72+2+2
f(-2) = 196

Edwin