Question 820390: According to a survey, college students make an average of 11 calls per day on their mobile
phone. Moreover, 80% of the students surveyed indicated that their parents pay for their
mobile phone expenses.
(a) If a student is selected at random, what is the probability that he or she makes:
(i) More than 12 calls in a day?
(ii) Less than the average number of calls in a day?
(iii) More than 15 calls in a day?
(b) If 20 students are selected at random, what is the probability that:
(i) All 20 have their parents pay for their mobile phone expenses?
(ii) At least 8 have their parents pay for their mobile phone expenses?
(iii) No more than 5 students pay for their own mobile phone expenses?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Re Reply, must refer You further to stattrek.com for their excellent tutorials
Formulas given below for Poisson and Binomial Distributions give a singular probability.
As all but one of the problems involved cumulative probabilities: Recommend using Ti Calculator to retrieve answers:
If You do not have access to a Ti Calculator, recommend stattrek.com (choosing Stat Tables will give you access to calculators
(also a good reference to check your Ti Calculations while You learn how to use it)
According to a survey, college students make an average of 11 calls per day on their mobile
phone. Moreover, 80% of the students surveyed indicated that their parents pay for their
mobile phone expenses.
(a) If a student is selected at random, what is the probability that he or she makes:
POISSON Distribution P(x; μ) = (e^(-μ) (μ^x) / x! where μ is the average number of successes
x is the actual number of successes that result from the experiment, e approximately equal to 2.71828.
for ex: μ = 11 P(x = 6) = 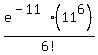
(i) More than 12 calls in a day? 0.31130334853593 Ti: 1- poissioncdf(11, 12)
P(x>12) = 1 - [P(1)+P(2)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+P(9)+P(10)+P(11)+P(12)]
(ii) Less than the average number of calls in a day? 0.459888702693687 poissioncdf(11, 10)
P(x<11) = [P(1)+P(2)+P(1)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+P(9)+P(10)]
(iii) More than 15 calls in a day? 0.092603908284245 Ti: 1- poissioncdf(11, 15)
BINOMIAL Distribution P(x) = nCx* 
where p and q are the probabilities of success and failure respectively.
In this case p = .80 & q = .20 & n = 20 nCx = 
For ex: b (i), P(20) =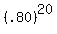
(b) If 20 students are selected at random, what is the probability that:
(i) All 20 have their parents pay for their mobile phone expenses? 0.0115292150460685 Ti binomcdf(20, .80, 20).
(ii) At least 8 have their parents pay for their mobile phone expenses?0.999984837159687 Ti 1 - binomcdf(20, .80, 7).
1 - [P(1)+P(2)+P(3)+P(4)+P(5)+P(6)+P(7)]
(iii) No more than 5 students pay for their own mobile phone expenses?0.804207785459551 Ti binomcdf(20, .20, 5).
[P(1)+P(2)+P(3)+P(4)+P(5)]
|
|
|