|
Question 819639: Sammy decided to go Christmas shopping at the mall. He had won a pass that allowed him to take an additional 20% off all final price purchases at any store, which he used for each purchase. First Sammy went to Game Stop to by his friend a video game. Game stop was having a 35% off store-wide sale. Then, he headed off to Payless to take advantage of their 25% off everything sale, to buy a pair of shoes. His last stop was at Moosejaw to buy a pullover, because they were having a one-day sale where everything was 15% off. As Sammy was leaving the mall, he stopped at a gift wrapping booth. They were charging $2.75(tax-included) for each gift wrapped. Sammy had all three gifts wrapped.
At the end of the month Sammy opened his credit card statement and noticed the following three charges:
Game Stop: $35.28
Payless: $55.72
Moosejaw: $96.89
What was the original price of each item AND what was the average dollar amount Sammy spent on each purchase?
Using MICHIGAN sales tax! 6%
What I already solved:
1. Work backwards
2. Undo the tax
3. $55.72 - $3.15 (tax)= $52.57
$35.28 - $2.54 (tax)= $32.74
$96.89 - $5.48 (tax)= $91.41
4. Undo the percent off
5. Total of 45% saved at Payless (25% + 20%)
Total of 55% saved at Game Stop (35% + 20%)
Total of 35% saved at Moosejaw (15% + 20%)
*This is the part of the process I don't understand
Found 2 solutions by rfer, KMST:
Answer by rfer(16322)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't think you can just add the discounted percent's because they are taken from different amounts.
take number three.
55.72-315=52.57
52.57/0.80=69.65
69.65/0.65=107.15 original price for payless
You do the other two and the averages.
You can see I used the price paid percentage, not the discount percentage.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ORIGINAL PRICE ON EACH ITEM:
The game at Game Stop was originally priced at $64.00.
For the sale, the store reduced the price by 35%, so the reduced price ended up being
100% - 35% = 65% of the original price
$ = $ = $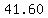 . .
The extra 20% from Sammy's pass reduced the price further by 20% calculated based on the $41.60 sale price.
That is a reduction of
$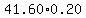 = $ = $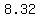
So Sammy ended up paying $41.60 - $8.32 = $33.28 (plus tax).
That $33.28 can be calculate directly as 80% of $41.60:
$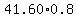 = $ = $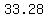
That twice reduced price is not 55% less than $64.00.
You cannot add percentages that are not applied to the same (original price.
Finally, the tax was calculated based on the final $33.28 price, and that increased the amount paid for the game by
$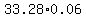 = $ = $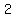 (rounded) for a total paid of (rounded) for a total paid of
$33.28 + $2.00 = $35.28, which is
100% + 6% = 106% of the final price,
which can be calculated directly by multiplying the final price by 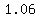
So, with all those percentages the original price was multiplied by  , then by , then by 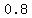 , and finally by , and finally by 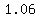 to get the final billed amount. to get the final billed amount.
If rounding errors from each step did not add up, the result would be the same as multiplying times
 , ,
which means that we could undo all the multiplications by dividing by 0.5512:
$35.28 ÷ 0.5512 = $64.01 (rounded)
For the shoes at payless the original price was reduced by 25%, to
100% - 25% = 75% of the original price.
That means that the original price was multiplied times 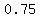 to get the sale price. to get the sale price.
Sammy's pass meant that the sale price was reduced by a further 20% to
100% - 20% = 80% of the already reduced sale price.
That means that the sale price was multiplied times 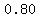 to get Sammy's final price. to get Sammy's final price.
Then 6% sales tax was added, increasing the amount Sammy paid to
100% +65 = 106% of the final special price Sammy got.
That means Sammy's special price was multiplied times 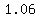 . .
To undo all those calculations, we can divide, first by 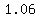 to undo the tax, then by to undo the tax, then by 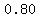 to undo the special 20% discount, and finally by to undo the special 20% discount, and finally by 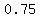 to undo the sale price reduction. to undo the sale price reduction.
We could even round at each step.
We can undo it all at once by dividing by

It should give the same result, or almost the same if roundings add up.
$55.72 ÷ 0.636 = $87.61
For the pullover bought at Moosejaw, the factor for the one-day sale 15% price reduction applied first is 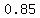 , and after that the same , and after that the same 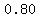 and and 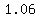 factors were applied to calculate Sammy's special discount and the price plus tax respectively. factors were applied to calculate Sammy's special discount and the price plus tax respectively.
The overall factor is
 and the original price was and the original price was
$96.89 ÷ 0.7208 = $134.42
|
|
|
| |