SOLUTION: A triangle ABC has sides with lengths a= 12 cm, b = 8 cm, and the angle B = 30º. What are the possible values for the length c of the third side of the triangle?

Algebra ->  Triangles -> SOLUTION: A triangle ABC has sides with lengths a= 12 cm, b = 8 cm, and the angle B = 30º. What are the possible values for the length c of the third side of the triangle?      Log On


   

Question 819293: A triangle ABC has sides with lengths a= 12 cm, b = 8 cm, and the angle B = 30º. What are the possible values for the length c of the third side of the triangle?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
ABC could be XBC OR YBC. vertex A could be X or Y, then side b (AB) would be XC or YC, measuring 8cm.
Since there were two possible triangles, I drew a third triangle, right triangle BCD.
CD = BCsin%2830%5Eo%29=12%2A0.5=6
We can also calculate
BD = BCcos%2830%5Eo%29=12%2A%28sqrt%283%29%2F2%29=6sqrt%283%29=about10.39
We can calculate the length of XD = YD in congruent right triangles XDC and YDC.
That length is
XD = YD =sqrt%288%5E2-6%5E2%29sqrt%2864-36%29=sqrt%2828%29=2sqrt%287%29=about5.29
Then,
BX = BD - XD =highlight%286sqrt%283%29-2sqrt%287%29%29= abouthighlight%285.10%29
BY = BD + YD =highlight%286sqrt%283%29%2B2sqrt%287%29%29= abouthighlight%2815.68%29
So the approximate measure of the third side is
either highlight%285.10cm%29 or highlight%2815.68cm%29 .

ALTERNATE SOLUTION:
Maybe your teacher expected you to use law of cosines,
b%5E2=a%5E2%2Bc%5E2-2ac%2Acos%28B%29
8%5E2=12%5E2%2Bc%5E2-2%2A12%2Ac%2Acos%2830%5Eo%29
64=144%2Bc%5E2-2%2A12%2Ac%2A%28sqrt%283%29%2F2%29
64=144%2Bc%5E2-%2812sqrt%283%29%29c
c%5E2-%2812sqrt%283%29%29c%2B144-64=0
c%5E2-%2812sqrt%283%29%29c%2B80=0
That quadratic equation can be solved using the quadratic formula:

The quadratic equation can also be solved by completing the square:
c%5E2-%2812sqrt%283%29%29c%2B80=0
c%5E2-%2812sqrt%283%29%29c=-80
c%5E2-%2812sqrt%283%29%29c%2B%286sqrt%283%29%29%5E2=%286sqrt%283%29%29%5E2-80
%28c-6sqrt%283%29%29%5E2=6%5E2%2A3-80
%28c-6sqrt%283%29%29%5E2=108-80
%28c-6sqrt%283%29%29%5E2=28 so ,
leading to the solutions highlight%28c=6sqrt%283%29+%2B-+2sqrt%287%29%29

ANOTHER ALTERNATE:
Since you have the measures of angle B and side b, you can apply law of sines, and find sin%28A%29, and two possible approximate measures for angle A.
Then you could calculate the approximate measures for the two options for angle C, and for 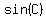sin%28C%29, and then use law of sines again to find the two possible measures for side c.