Question 81907: During rush hour, Fernando can drive 20 miles using the side roads in the same time that it takes to travel 15 miles on the freeway. If Fernando's rate on the side roads is 9 mi/h faster than his rate on the freeway, find his rate on the side roads.
A) 38 B) 36 C) 27 D) 29
Found 2 solutions by stanbon, ankor@dixie-net.com:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! During rush hour, Fernando can drive 20 miles using the side roads in the same time that it takes to travel 15 miles on the freeway. If Fernando's rate on the side roads is 9 mi/h faster than his rate on the freeway, find his rate on the side roads.
----------
Side road DATA:
distance = 20 mi ; Rate = x+9 mph ; time = d/r = 20/(x+9) hrs.
---------------
Freeway DATA:
distance = 15 mi ; Rate = x mph ; time = d/r = 15/x hrs.
--------------
EQUATION:
time = time
20/(x+9) = 15/x
20x = 15x+135
5x = 135
x = 27 mph (rate on freeway)
x+9 = 36 mph (rate on side roads)
=========
Cheers,
Stan H.
A) 38 B) 36 C) 27 D) 29
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! During rush hour, Fernando can drive 20 miles using the side roads in the same time that it takes to travel 15 miles on the freeway. If Fernando's rate on the side roads is 9 mi/h faster than his rate on the freeway, find his rate on the side roads.
:
Let s = speed on the side road. Let (s-9) = speed on the freeway
:
Write a time equation, Time = Distance/Speed
:
Side road time = Freeway time
 = = 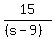
:
Cross multiply:
20(s-9) = 15s
20s - 180 = 15s
20s - 15s = 180
5s = 180
s = 180/5
s = 36 mph on the side road
:
Check the times on both speeds, 36 mph and 27 mph:
20/36 = .56 hrs
15/27 = .56 hrs; must be right!
|
|
|