SOLUTION: Express 3+9x-x^2 in the form of q-(x+r)^2,where q and r are constants.Hence (a)sketch it's extreme value and the value of x when this occurs, (b)sketch the curve y=3+9x-x^2 I

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Express 3+9x-x^2 in the form of q-(x+r)^2,where q and r are constants.Hence (a)sketch it's extreme value and the value of x when this occurs, (b)sketch the curve y=3+9x-x^2 I      Log On


   

Question 818813: Express 3+9x-x^2 in the form of q-(x+r)^2,where q and r are constants.Hence
(a)sketch it's extreme value and the value of x when this occurs,
(b)sketch the curve y=3+9x-x^2
I have found the values of q and r,but do not know what is extreme value and what does it mean.Please Help.
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
The curve is a parabola. The x-coordinate of the parabola's vertex (the extreme value other than the extremes at the end (+ or - infinity) is given by -b/2a where a is the coefficient of the x%5E2 term and b is the coefficient of the x term.


For this equation a = -1 and b = 9 (c=3, but we won't use it until later). -b/2a = -9/-2 = 9/2.


Plug it back into the equation to find the y coordinate.


3+9*9/2-81/4 = 93/4. The vertex is (9/2,93/4).


Find the x - intercepts, where the parabola crosses the x-axis, using the quadratic equation 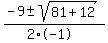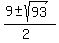x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ = %28-9+%2B-+sqrt%28+81%2B12+%29%29%2F%282%2A-1%29+ = %289+%2B-+sqrt%2893%29%29%2F%282%29+ = approximately -.322 and 9.270.


Plot the vertex and the intercepts. Draw the curve.