SOLUTION: Write the expression as a single log? 21log3 (cuberoot(x)) + log3 (9x^2) - log5 25 Thanks!

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Write the expression as a single log? 21log3 (cuberoot(x)) + log3 (9x^2) - log5 25 Thanks!      Log On


   

Question 818477: Write the expression as a single log?
21log3 (cuberoot(x)) + log3 (9x^2) - log5 25
Thanks!
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I'm assuming that the numbers immediately after "log" are supposed to be the bases of these logs. If I am wrong, then you will have to re-post your question. In the future, either use some English to describe your logs (like "base 5 log of (25) for 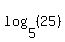log%285%2C+%2825%29%29, or teach yourself algebra.com's syntax for formulas. (Click on the "Show source" link above to see what I typed to get that logarithm to display so nicely.)


The following properties of logarithms are often used in problems like this:
  • log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Aq%29%29
  • log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Fq%29%29
  • n%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5En%29%29
The first two are used to combine logs. They require that the logs have the same bases and coefficients of 1. The third property, since it allows us to "move" a coefficient out of the way, is often used to get coefficients of 1 so the other two properties may be used.

The first log has a coefficient that is not a 1, it is 21. So we will use the third property to move the 21 into the argument as its exponent:

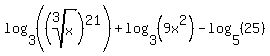
We can use fractional exponents to simplify the first argument. Since a cube root is the same as an exponent of 1/3:

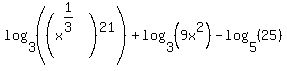
The rule for powers of a power is to multiply. Since 1/3*21 = 7:
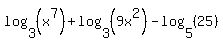
log%283%2C+%28x%5E7%29%29+%2B+log%283%2C+%289x%5E2%29%29+-+log%285%2C+%2825%29%29

Now we can use the first property to combine the first two logs:
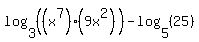
log%283%2C+%28%28x%5E7%29%2A%289x%5E2%29%29%29+-+log%285%2C+%2825%29%29
which simplifies to:
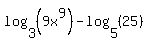
log%283%2C+%289x%5E9%29%29+-+log%285%2C+%2825%29%29

We cannot use the second property to combine the remaining logs because the bases are different, 3 and 5. But the second log is one we can figure out "by hand". 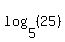log%285%2C+%2825%29%29 represents the exponent one would put on a 5 to get a result of 25. We know what this exponent is. It is 2. So log%285%2C+%2825%29%29+=+2. This makes our expression:
log%283%2C+%289x%5E9%29%29+-+2
This might be an acceptable answer. It is an expression with a single logarithm. But the problem, as you posted it, says "express as a single log" not "express with a single log" like we have above. If the final answer is really supposed to be just a single log and nothing else, then we have some more work to do.

Here we can use a little trick. We are going to turn the "2" into a logarithm with a base of 3. This will allow us to combine the remaining terms into a single logarithm. log%283%2C+%283%29%29+=+1 since the exponent for 3 that results in a 3 is 1. So I will multiply the 2 by (a weird-looking) 1:
log%283%2C+%289x%5E9%29%29+-+2%2Alog%283%2C+%283%29%29
Now we use the third property to get the coefficient of 2 out of the way:
log%283%2C+%289x%5E9%29%29+-+log%283%2C+%28%283%29%5E2%29%29
which simplifies to:
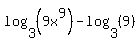
log%283%2C+%289x%5E9%29%29+-+log%283%2C+%289%29%29
Now we can use the second property to combine the terms:
log%283%2C+%28%289x%5E9%29%2F9%29%29
The factors of 9 cancel:
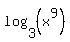
log%283%2C+%28x%5E9%29%29