Question 818283: "compute the exact values of sin 2x, cos 2x, tan 2x without a calculator. Cos x= (-4/5), pi/2
So far I have figured out that I need to use the identities sin 2x= 2sin x cos x, cos 2x=cos^2 x - sin^2 x
For the first identity I swap out cos X with -4/5, but I do not know how to get sin x so I can figure out sin 2x. If you could help me out I would be greatly indebted to you! thanks!
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website! "compute the exact values of sin(2θ), cos(2θ), tan(2θ) without a calculator.
cos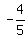(θ)= ,  < θ <  .
's
I changed your x's to θ so that x could represent the values on the
x-axis rather than the angle.
------------------------------------------------------
We draw the angle θ in the second quadrant.
And we draw a perpendicular to the x-axis from the end of the green line
forming a right triangle.
The bottom side of the triangle is x
The vertical side of the triangle is y,
and the green line is r.
The cosine is  and we are given that cos(θ)=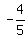
so we will take x as the numerator, considering it negative, since it
goes to the left. So we will label it x=-4, and we will label r as
the denominator of 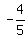, considering it positive, since it goes
up. So we will label it as r=5
We calculate y from
r² = x²+y²
5² = (-4)²+y²
25 = 16+y²
9 = y²
±3 = y, we take the positive value since y goes up.
So we label the y-value as 3
sin(2θ) = 2sin(θ )cos(θ )
Since sin(θ ) =  , sin(θ ) = 
sin(2θ) = 2sin(θ )cos(θ ) = 2 =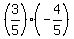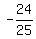 
cos(2θ) = cos²(θ)-sin²(θ) =  - =  - = 
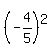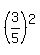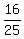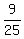tan(2θ) =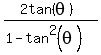 
Since the tangent is  , tan(θ) =  = 
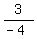tan(2θ) =  =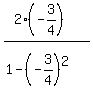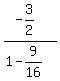 
Multiply top and bottom by 16
tan(2θ) =  =  =  = 
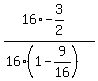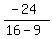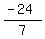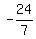Edwin
|
|
|
