SOLUTION: Please help me solve this equation: Find all asymptotes, intercepts and graph. you must also find all the critical points and inflections points (if any) f(x) = x^3-3x^2-10x/

Algebra ->  Rational-functions -> SOLUTION: Please help me solve this equation: Find all asymptotes, intercepts and graph. you must also find all the critical points and inflections points (if any) f(x) = x^3-3x^2-10x/      Log On


   

Question 816619: Please help me solve this equation:
Find all asymptotes, intercepts and graph. you must also find all the critical points and inflections points (if any)
f(x) = x^3-3x^2-10x/x^2+5x+6
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!


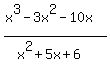f(x) = %28x%5E3-3x%5E2-10x%29%2F%28x%5E2%2B5x%2B6%29

Factor the numerator:     Factor the denominator

    x³-3x²-10x                x²+5x+6                    
    x(x²-3x-10)              (x+3)(x+2)
    x(x+3)(x+2)

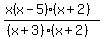f(x) = %28x%28x-5%29%28x%2B2%29%29%2F%28%28x%2B3%29%28x%2B2%29%29

Since (x+3) is a factor of the denominator but not
the numerator, there is an asymptote where x+3=0,
or at x=-3, which is the equation of the vertical
asymptote, where there is a non-removable discontinuite.
 Since (x+2) is a factor of both denominator and numerator,
there is a removable discontinuity where x+2=0, at x=-2.

We may cancel the (x+2)'s as long as we also state that
x≠2

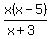f(x) = x%28x-5%29%2F%28x%2B3%29, where x≠2

So we graph

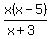y = x%28x-5%29%2F%28x%2B3%29, leaving a hole at x=2

There is a vertical asymptote at x=-3
Since the degree of the numberator is 1 more than the degree
of the denominator, there is no horizontal asymptote, but there
is an oblique (or slant) asymptote, which we find by long
division:

We have to multiply the numerator out and add +0 to divide:

y = x%B2-5x%2B0%29%2F%28x%2B3%29,

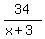        x- 8+34%2F%28x%2B3%29
x+3)x²-5x+ 0
    x²+3x
      -8x+ 0
      -8x-24
          34

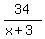Since the fraction 34%2F%28x%2B3%29 approaches 0 as x gets large,
the graph of f(x) must approach the line y=x-8, which is the
equation of the oblique (slant) asymptote.

We get the y-intercept by setting x = 0

y = 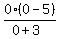0%280-5%29%2F%280%2B3%29 = 0

So the y-intercept is (0,0)

We get the x-intercepts by setting y = 0 

0 = 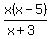x%28x-5%29%2F%28x%2B3%29

0 = x(x-5)
    x=0;  x-5=0
            x=5

So the x-intercepts are (0,0) and (5,0)

We plot the asymptotes and the intercepts:


 

Now we find any relative extrema points by
finding the derivative and setting it = 0

y = %28x%28x-5%29%29%2F%28x%2B3%29
Multiply the top out:
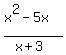y = %28x%5E2-5x%29%2F%28x%2B3%29
Use the quoptient formula for the derivative:
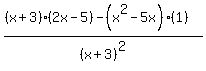y' = %28%28x%2B3%29%282x-5%29-%28x%5E2-5x%29%281%29%29%2F%28x%2B3%29%5E2
y' = %282x%5E2-5x%2B6x-15-x%5E2%2B5x%29%2F%28x%2B3%29%5E2
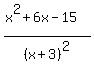y' = %28x%5E2%2B6x-15%29%2F%28x%2B3%29%5E2
Setting that = 0 to find relative extrema:
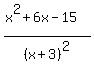%28x%5E2%2B6x-15%29%2F%28x%2B3%29%5E2 = 0
x²+6x-15 = 0
Unfortunately that doesn't factor, so we must
use the quadratic formula:
x+=+%28-6+%2B-+sqrt%28+6%5E2-4%2A1%2A%28-15%29+%29%29%2F%282%2A1%29+
x+=+%28-6+%2B-+sqrt%2836%2B60%29%29%2F2+
x+=+%28-6+%2B-+sqrt%2896%29%29%2F2+
x+=+%28-6+%2B-+sqrt%2816%2A6%29%29%2F2+
x+=+%28-6+%2B-+4sqrt%286%29%29%2F2+
x+=+%282%28-3+%2B-+2sqrt%286%29%29%29%2F2+
x+=+%28cross%282%29%28-3+%2B-+2sqrt%286%29%29%29%2Fcross%282%29+
x = -3 ± 2V6
Approximating:  x=-7.90 and x=1.90
Substuting those in y, we get approximately
                y=-20.8 and y=-1.20

Relative extrema candidates are approximately (-7.90,-20.8)
and (1.90,-1.20)

To find out whether they are relative maximums or minimums,
or any inflection points, we must find the second derivative:

y' = 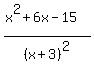%28x%5E2%2B6x-15%29%2F%28x%2B3%29%5E2
Use the quotient formula:
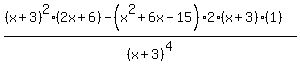y" = %28%28x%2B3%29%5E2%282x%2B6%29-%28x%5E2%2B6x-15%292%28x%2B3%29%281%29%29%2F%28x%2B3%29%5E4
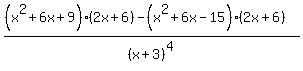y" = %28%28x%5E2%2B6x%2B9%29%282x%2B6%29-%28x%5E2%2B6x-15%29%282x%2B6%29%29%2F%28x%2B3%29%5E4
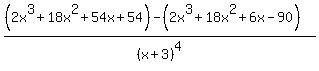y" = %28%282x%5E3%2B18x%5E2%2B54x%2B54%29-%282x%5E3%2B18x%5E2%2B6x-90%29%29%2F%28x%2B3%29%5E4  
y" = %282x%5E3%2B18x%5E2%2B54x%2B54-2x%5E3-18x%5E2-6x%2B90%29%2F%28x%2B3%29%5E4
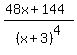y" = %2848x%2B144%29%2F%28x%2B3%29%5E4
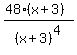y" = %2848%28x%2B3%29%29%2F%28x%2B3%29%5E4
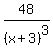y" = 48%2F%28x%2B3%29%5E3

Substituting x=-7.90, y" comes out negative,
therefore the point (-7.90,-20.8) is a relative
maximum, since the curvature is downward

Substituting x=1.90, y" comes out positive,
therefore the point (1.90,-1.20) is a relative
minimum, since the curvature is upward
 
To find any inflection points we set y"=0

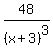48%2F%28x%2B3%29%5E3 = 0
48 = 0
A contradiction so there are no inflection points.

So we draw the graph:

 

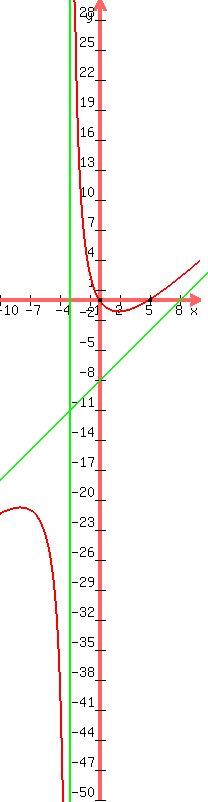What a terribly long and messy problem!

Edwin