|
Question 815898: A christmas tree vendor sells evergreen trees at $40 each and artifical trees at $65 each. A total of 62 trees were sold for a total of $2,930. Find the number each type of trees that were sold. Solve problem using determinants.
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! "You listed this as "Matrices, determinant, Cramer Rule", but nothing fancy is really needed for this fairly simple problem, so hopefully my posting a solution guide is not disrupting the kind of response you want.
x and y for everygreens and artificial, respectively.
Accounting for trees, x+y=62.
Accounting for money, 40x+65y=2930.
Simplify the money equation: 8x+13y=586;
Your system is best given as the equations:  and and  . .
You might want to make a matrix,
( 1, 1, 62 )
( 8, 13, 586 )
Do this row replacement: R2=R2-8*R1; this is basically an elimination step.
The result should be a quick step to solve for y. As a matrix, you can express
( 1, 1, 62 )
( 8-8*1, 13-8*1, 586-8*62 )
=
( 1, 1, 62 )
( 0 , 5, 90 )
'
The second row now indicates 5y=90; you could now multiply the entire second row by 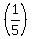 and you would have accomplished solving for y. and you would have accomplished solving for y.
----------------------------------
Do not let confusion happen. I am not indicating points or such but vectors of a matrix and the use of the commas is to help read where one element begins and ends
|
|
|
| |