Question 815509: Find all the rational roots for:  , when P(x)=0.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
To find roots of a polynomial, rational or not, you need to factor the polynomial. Unfortunately none of the factoring techniques appear to work on this polynomial except for trial and error of the possible rational roots.
So we will start by listing the possible rational roots. The possible rational roots to a polynomial are all the possible ratios, positive and negative, that can be formed using a factor of the constant term in the numerator and a factor of the leading coefficient in the denominator. P(x)'s constant term is 15. (Actually it is -15 but since we're going to use all positive and negative ratios anyway, it does not matter if we use 15 or -15.) The factors of 15 are 1, 3, 5 and 15. P(x)'s leading coefficient is 6. Its factors are 1, 2, 3 and 6. This makes the possible rational roots:
+1/1, +3/1, +5/1, +15/1, +1/2, +3/2, +5/2, +15/2, +1/3, +3/3, +5/3, +15/3, +1/6, +3/6, +5/6 and +15/6.
Simplifying and removing the duplicates we get:
+1, +3, +5, +15, +1/2, +3/2, +5/2, +15/2, +1/3, +5/3, +1/6 and +5/6.
We can use synthetic division to test these. First we'll try 1:
1 | 6 -13 13 -39 -15
---- 6 -7 6 -33
--------------------------
6 -7 6 -33 -48
The number in the lower right corner is the remainder. It is not zero so 1 is not a root (and (x-1) is not a factor) of P(x). Next we'll try 3:
3 | 6 -13 13 -39 -15
---- 18 15 84 135
--------------------------
6 5 28 45 120
Again a remainder that is not zero. So 3 is not a root (and (x-3) is not a factor) of P(x). Since the remainder for 1 was negative and the remainder for 3 was positive, there must be a root between 1 and 3. So I'll try some fractions between 1 and 3. Since the remainder for 1 is closer to zero than the remainder for 3 I'll try fractions that are closer to 1. Like 3/2:
3/2| 6 -13 13 -39 -15
---- 9 -6 21/2 -171/4
--------------------------
6 -4 7 -57/2 negative
Another negative remainder. So there is a root between 3/2 and 3. Let's try 5/2 next:
5/2| 6 -13 13 -39 -15
---- 15 5 45 15
--------------------------
6 2 18 6 0
And we finally have a winner! 5/2 is a root and (x-5/2) is a factor. Not only that, the rest of the bottom row tells us the other factor. The "6 2 18 6" translates into 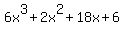 . At this point we have:
We could continue to do trial and error factoring on 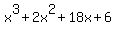 . But it will factor by grouping (which I think is easier):
The last factor will not factor further so we will get no more rational roots from it. From the first two factors we have rational roots of 5/2 and -1/3.
|
|
|
