SOLUTION: On a shelf there are four Mathematics books and eight English books. How many ways can the books be arranged? What is the probability that all the Mathematics books will not be arr

12! = 479001600
/pre>
What is the probability that all the Mathematics books will not be arranged together?
We will get the probability of the complement event -- the probability
of one of these 9 ways occurring where the math books are all together.

MMMMEEEEEEEE, EMMMMEEEEEEE, EEMMMMEEEEEE, EEEMMMMEEEEE, EEEEMMMMEEEE,
EEEEEMMMMEEE, EEEEEEMMMMEE, EEEEEEEMMMME, EEEEEEEEMMMM.

In each of those 9 ways the Math books can be arranged 4! ways and the
English books can be arranged 8! ways. The probability that they will be
together is 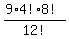  = 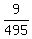 =  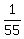= 0.0181818182.

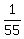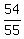So the probability that they will NOT all be together is 1- =  = .9818181818.

Edwin