SOLUTION: Hi I've been trying to find out what to do and how to do and I'm stuck so I'm hoping you can help me Simplify the right-hand side of the equation What is f of x equal x square

Algebra ->  Rational-functions -> SOLUTION: Hi I've been trying to find out what to do and how to do and I'm stuck so I'm hoping you can help me Simplify the right-hand side of the equation What is f of x equal x square       Log On


   

Question 815092: Hi I've been trying to find out what to do and how to do and I'm stuck so I'm hoping you can help me
Simplify the right-hand side of the equation
What is f of x equal x square plus seven x plus ten over x square subtract seven x subtract eighteen
It looks like F(x) = x^2+7x+10
---------------------- x^2-7x-18
And please show every step that will help so much thank you
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Are you asking for a simplification of F%28x%29=%28x%5E2%2B7x%2B10%29%2F%28x%5E2-7x-18%29 ?

Factorize the numerator and denominator. Look for common factors which are equivalent to a factor of 1. Just be aware than if you cancel these, the meaning of the simplified form will be changed.

Numerator: (x+2)(x+5)
Denominator: (x+2)(x-9)

The function can be rewritten, F%28x%29=%28%28x%2B2%29%28x%2B5%29%29%2F%28%28x%2B2%29%28x-9%29%29.
BEFORE simplification, you must understand that the function has a skipped point at x=-2 and an asymptote at x=9.

The simplification is to cancel the apparant %28x%2B2%29%2F%28x%2B2%29 as a factor of 1:
highlight%28h%28x%29=%28x%2B5%29%2F%28x-9%29%29.
You will note that I changed the name of this function. The discontinuity at x=-2 is now gone, so the h(x) IS continuous there, but the asymptote at x=9 remains for h(x) as it does for F(x).

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
f(x) = 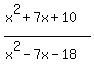%28x%5E2%2B7x%2B10%29%2F%28x%5E2-7x-18%29

Since the degree of the numerator and denominator are both 2,
the horizontal asymptote has the equation

y = %28LEADING_COEFFICIENT_OF_NUMERATOR%29%2F%28LEADING_COEFFICIENT_OF_DENOMINATOR%29

y = 1%2F1

y = 1

Let's draw the horizontal asymptote y = 1 (in green) 



This function f(x) is not defined when the denominator = 0.
It either has a vertical asymptote there or else it
has a hole in the curve.

We set the denominator = 0.

  x²-7x-18 = 0
(x-9)(x+2) = 0
x-9=0;  x+2=0
  x=9;    x=-2

So the function is not defined at either x=9 or x=-2.

The domain of f(x) is (-oo,-2)U(-2,9)U(9,oo)

Next we find out if there is a vertical asymptote or
a "hole in the curve" (removable discontinuity)
at x=9 and x=-2

Factor the numerator x²+7x+10 as (x+5)(x+2)
We have already factored the denominator x²-7x-18 as (x-9)(x+2).


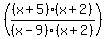f(x) = %28%28x%2B5%29%28x%2B2%29%2F%28x-9%29%28x%2B2%29%29

Now we may ONLY cancel the (x+2)'s if we specify that x is not
equal to -2, for f(x) is not defined at x=-2 or at x=9.

But the fact that we have a factor (x-2) in the numerator and 
also an (x-2) factor in the denominator tells us there is a
removable discontinuity at x=-2.  And since there is no (x-9)
factor in the numerator tells us that there is a vertical
asymptote at x=9.

So we draw the vertical asymptote (also in green) which has 
the equation x=9


 

Now if we cancel the (x+2)'s we will get a function that we will
call g(x).  g(x) is exactly like f(x) except it will have a value at 
x=2 whereas f(x) does not have a value there.

So the graph that removes the dicontinuity (plugs up the hole) is

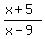g(x) = %28x%2B5%29%2F%28x-9%29 has an asymptote at x=9

Let's first draw g(x), which does not have a hole:



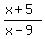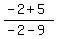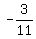In fact when x=-2 we have g(-2)=%28x%2B5%29%2F%28x-9%29=%28-2%2B5%29%2F%28-2-9%29=-3%2F11%29


But we don't want g(x), we want f(x), so we must put a hole in
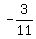the curve at the point (-2,-3%2F11), for that is a removable
discontinuity.  



Edwin