|
Question 814829: Please help me sketch the following function by determining the critical points as follows: f(x)=sqrt(x-4): the domain and intercepts
Answer by josgarithmetic(39620)   (Show Source):
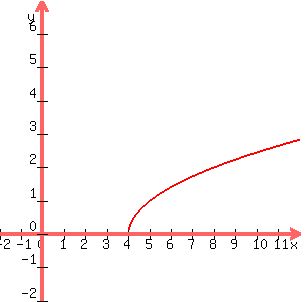
You can put this solution on YOUR website! Not sure if it is called a critical point, but  is a requirement in Real Numbers for the domain of f(x). The far-left point is the one which intersects the x axis, at (4,0). In other way of saying,  . No other axis intercepts.
Hopefully, a better explanation:
-----------------------------------------------------------------
DOMAIN: What value are acceptable for x?
Square Root function for real numbers must accept positive values for zero. Negative values are not acceptable.
 must have  which means  or .
This means, the DOMAIN of f(x) is  .
Checking for intercepts, at x=0, what is f(x)?
 , NOT acceptable because 0 is not in the domain of f(x). Recall, we just found that the domain of f(x) is , and 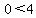 , so x cannot be 0. This means, f(x) will not cross the y-axis.
'
What about f(x)=0? What would x be for this?
Square both sides,
This is the point, (4,0) as the x-intercept.
Your will recognize the equation as half of a parabola with horizontal axis of symmetry:
|
|
|
| |
