SOLUTION: if 3^(8n+3) divided by 5 what will be the remainder,where n is a integer

If n=1, we have 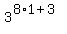 =  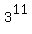= 177147, when divided by 5, has remainder 2.

That is 

We will try to prove, by induction, that the remainder will always be 2.

That is, we will try to prove  for some integer p

Assume that for all , 

(1)       for some integer p       <--assumed

we want to use (1) to prove: 

          for some integer q   <--unproved 

or

          for some integer q     <--unproved

or

(2)      for some integer q       <--unproved

We want to show that the assumption of (1) imples (2)

Multiply both sides of (1) by 3^8

        

        

        

         

        

So we take integer  and we have proved (2)

(2)      for some integer q

Therefore the remainder is 2 for all n

Edwin