Question 81409This question is from textbook Precalculus
: the frog population in a small pond grows exponentially. The current population is 85 frogs, and the relative growth rate is 18% per year.
a. find function that models the population after t years.
b. find the projected population after 3 years.
c. find the number of years required for the frog population to reach 600.
This question is from textbook Precalculus
Found 2 solutions by stanbon, SMM52091:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! the frog population in a small pond grows exponentially. The current population is 85 frogs, and the relative growth rate is 18% per year.
a. find function that models the population after t years.
A(t) = A(0)(1.18)^t
A(t) = 85(1.18)^t
----------
b. find the projected population after 3 years.
A(3) = 85(1.18)^3
A(3)= 139.65 frogs
Rounding down: 139 frogs
--------------------
c. find the number of years required for the frog population to reach 600.
600 = 85(1.18)^t
7.0588=1.18^t
Take the log of both sides to ge:
t=[log7.0588]/[log1.18]
t=11.81 years
================
Cheers,
Stan H.
Answer by SMM52091(3)   (Show Source): (Show Source):
You can put this solution on YOUR website! Forumula for this type of problem would be  where P is the new amount, e is the original, r is the rate, and t is the time. You can create that formula by simply thinking about what the question is asking. If one year goes by, then the new amount of frogs is 18% greater, or where P is the new amount, e is the original, r is the rate, and t is the time. You can create that formula by simply thinking about what the question is asking. If one year goes by, then the new amount of frogs is 18% greater, or  OR OR 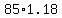 . If two years go by, then you'd get . If two years go by, then you'd get 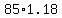 after year one, and then multiply that by 1.18 AGAIN for the second year, so technically after year one, and then multiply that by 1.18 AGAIN for the second year, so technically 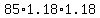 Also known as Also known as 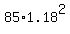 So.... So....
a) the formula as a function would be... 
b) plug in to find out the population after 3 years (t)


 Don't forget to round off, because you can't have .65772 of a frog, thats ridiculous. So 140 frogs after 3 years Don't forget to round off, because you can't have .65772 of a frog, thats ridiculous. So 140 frogs after 3 years
c)plug in to find out the amount of f(t) = 600





It would take 11.80729861 years to reach 600 frogs.
|
|
|