Question 813935: Please help me solve these two problems log(2x+9)=1+log(x-9)and log(6)square root of x - log(4)^2
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! log(2x+9)=1+log(x-9)
A general procedure for solving these kinds of equations:- Use algebra and/or properties of logarithms to transform the equation into one of the following forms:
- log(expression) = other-expression
- log(expression) = log(other-expression) (Note: The bases of the two logs must match.)
- Eliminate the logarithms:
- If the equation is in the first form, "log(expression) = other-expression", rewrite the equation in exponential form.
- If the equation is in the second form, "log(expression) = log(other-expression)", set the arguments equal.
- Now that the logs are gone, solve the equation (using techniques which are appropriate for the type of equation it is).
- Check your solution. This is not optional! A check must be made to see if the bases and arguments of all logs are valid. Any "solution" which make any base or an argument invalid must be rejected! (Note: Valid bases are positive but not 1 and valid arguments are positive.)
Let's try this on your equation. First we decide which form we think will be easiest to achieve. With the "non-log" term of 1 (on the right side), it would seem that the second, "all-log" form will be harder to reach. So we will aim for the first form.
Stage 1: Transform
To reach this form, all we need to do is find a way to combine all the logs into a single logarithm. We will getting them both on the same side of the equation. Subtracting log(x-9) from each side:
log(2x+9)-log(x-9)=1
Now we can use the  property to combine them: property to combine them:

And we have reached the first form.
Stage 2: Eliminate the logs.
With the first form we just rewrite the equation in exponential form. In general  is equivalent to is equivalent to  . Using this pattern, and the fact that the base of "log" is 10, we get: . Using this pattern, and the fact that the base of "log" is 10, we get:

which simplifies to:

Stage 3: Solve
We'll start by eliminating the fraction (by multiplying each side by (x-9):

which simplifies to:'

Subtracting 2x:

Adding 90:

Divide by 8:

Stage 4: Check
Use the original equation to check:
log(2x+9)=1+log(x-9)
Checking x = 99/8:

Simplifying:


At this point we can see that both arguments are or are going to be positive (i.e. valid). And the bases are valid so this solution checks out! x = 77/8.
I can't help you with the second problem because:- You didn't include the instructions. What are you/we supposed to do with this?
- I can't tell if the equation is:
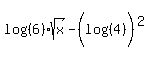
or
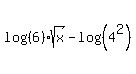
or

etc.
Please- Use parentheses generously to group things like function arguments, exponents, numerators and denominators together so that the meaning of the expression cannot be confused.
- If posting logarithms with bases other than 10 ("log") or e ("ln"), either use some English (like "base 6 log of the square root of (x)" or teach yourself how to use algebra.com's formula syntax. Clink on the "Show source" link above to see what I typed to get:
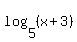
to display like it does.
|
|
|