SOLUTION: Please help me solve these two problems log(2x+9)=1+log(x-9)and log(6)square root of x - log(4)^2

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Please help me solve these two problems log(2x+9)=1+log(x-9)and log(6)square root of x - log(4)^2      Log On


   

Question 813935: Please help me solve these two problems log(2x+9)=1+log(x-9)and log(6)square root of x - log(4)^2
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
log(2x+9)=1+log(x-9)

A general procedure for solving these kinds of equations:
  1. Use algebra and/or properties of logarithms to transform the equation into one of the following forms:
    • log(expression) = other-expression
    • log(expression) = log(other-expression) (Note: The bases of the two logs must match.)
  2. Eliminate the logarithms:
    • If the equation is in the first form, "log(expression) = other-expression", rewrite the equation in exponential form.
    • If the equation is in the second form, "log(expression) = log(other-expression)", set the arguments equal.
  3. Now that the logs are gone, solve the equation (using techniques which are appropriate for the type of equation it is).
  4. Check your solution. This is not optional! A check must be made to see if the bases and arguments of all logs are valid. Any "solution" which make any base or an argument invalid must be rejected! (Note: Valid bases are positive but not 1 and valid arguments are positive.)
Let's try this on your equation. First we decide which form we think will be easiest to achieve. With the "non-log" term of 1 (on the right side), it would seem that the second, "all-log" form will be harder to reach. So we will aim for the first form.

Stage 1: Transform
To reach this form, all we need to do is find a way to combine all the logs into a single logarithm. We will getting them both on the same side of the equation. Subtracting log(x-9) from each side:
log(2x+9)-log(x-9)=1
Now we can use the log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29+=+log%28a%2C+%28p%2Aq%29%29 property to combine them:
log%28%28%282x%2B9%29%2F%28x-9%29%29%29=1
And we have reached the first form.

Stage 2: Eliminate the logs.
With the first form we just rewrite the equation in exponential form. In general log%28a%2C+%28p%29%29+=+n is equivalent to p+=+a%5En. Using this pattern, and the fact that the base of "log" is 10, we get:
%282x%2B9%29%2F%28x-9%29=10%5E1
which simplifies to:
%282x%2B9%29%2F%28x-9%29=10

Stage 3: Solve
We'll start by eliminating the fraction (by multiplying each side by (x-9):
2x%2B9=%28x-9%2910
which simplifies to:'
2x%2B9=10x-90
Subtracting 2x:
9=8x-90
Adding 90:
99=8x
Divide by 8:
99%2F8=x
Stage 4: Check
Use the original equation to check:
log(2x+9)=1+log(x-9)
Checking x = 99/8:
log%28%282%2899%2F8%29%2B9%29%29=1%2Blog%28%28%2877%2F8%29-9%29%29
Simplifying:
log%28%282%2899%2F8%2B72%2F8%29%29%29=1%2Blog%28%2877%2F8-72%2F8%29%29
log%28%282%28171%2F8%29%29%29=1%2Blog%28%285%2F8%29%29
At this point we can see that both arguments are or are going to be positive (i.e. valid). And the bases are valid so this solution checks out! x = 77/8.

I can't help you with the second problem because:
  • You didn't include the instructions. What are you/we supposed to do with this?
  • I can't tell if the equation is:
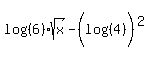
    log%28%286%29%29%2Asqrt%28x%29+-+%28log%28%284%29%29%29%5E2
    or
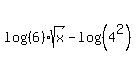
    log%28%286%29%29%2Asqrt%28x%29+-+log%28%284%5E2%29%29
    or
    log%286%2C+%28sqrt%28x%29+-+%28log%284%29%29%5E2%29%29
    etc.
    Please
    • Use parentheses generously to group things like function arguments, exponents, numerators and denominators together so that the meaning of the expression cannot be confused.
    • If posting logarithms with bases other than 10 ("log") or e ("ln"), either use some English (like "base 6 log of the square root of (x)" or teach yourself how to use algebra.com's formula syntax. Clink on the "Show source" link above to see what I typed to get:
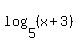
      log%285%2C+%28x%2B3%29%29
      to display like it does.