Question 81388: I am taking an online electronics course and I am stumped on decibel/logarithm section relating to amplifiers. My problems deal in power or voltage gain, and levels. Here are 2 examples that I cannot solve. (1) A power amplifier has a gain of 26dB, and an input of 1 volt. What is the voltage level? (2) An amplifier has a voltage gain of 60dB, the input is 10 microvolts, what is the output? I have a couple formulas, and I know the answers, but I can't figure out how to get the answers from the formulas. The answer to problem one is 20, and the answer to problem 2 is 10. Here are the formulas:
Gain= signal out/signal in
dB= 10 x log(base 10) (W out/ W in)
dB= 20 x log(base 10) (V out/ V in)
Output voltage= input level x gain ratio
I need a very detailed expression as to how to solve these problems. I have looked in two textbooks for further explanation, but I cannot find the solutions.
Thank you so much if you can help!!!!
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve these two problems you need only the voltage amplification equation:
.

.
and a knowledge of a few rules of Logarithms.
.
The dB equation defines decibels. It uses the base 10 Logarithms. In this equation,
 is the output voltage, and is the output voltage, and  is the input voltage. is the input voltage.
.
Here are a couple of rules of Logarithms that you should be familiar with. Assume that
the base of the Logarithm is b:
.
Rule I.
. 
.
Rule II.
.  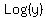
.
Rule III.
.  + + 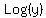
.
Rule IV.
. Log base b of x = y is equivalent to saying 
.
Note that in decibel calculations b (the base) is 10. This translates Rule IV to:
.
Log (x) = y is equivalent to saying 
.
If you need a further explanation of these rules, you can get it from an Algebra II text,
from elsewhere on this site, or by doing a Google on Logarithms.
.
Time to work your first problem by using the voltage form of the decibel equation.
Given the amplifier has a power gain of 26 dB, and an input voltage of 1 volt. Substitute
those two values into the dB equation (26 for dB and 1 for the input voltage) and you get:
.

.
The plan is to work down to  , so start by dividing both sides of this equation by , so start by dividing both sides of this equation by
20 to get rid of the 20 on the right side. At the same time note that 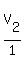
is just  . These simplifications lead to the equation becoming: . These simplifications lead to the equation becoming:
.

.
And after dividing 26 by 20 on the left side the equation reduces to:
.

.
Time to apply Rule IV. When you do you get:
.

.
Calculator time. Your calculator probably works this way: enter 1.3 then press the 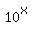
key and you find the result to be 19.95262315 volts. Close enough for electrical work.
Call it 20 volts.
.
Now to your second problem. If the answer is to be 10, then you probably meant that the
input voltage was 10 millivolts 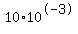 instead of 10 microvolts instead of 10 microvolts 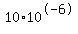 . .
So lets use 10 millivolts.
.
For the given gain of 60 dB and an input of 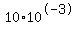 volts the equation becomes: volts the equation becomes:
.

.
Just as was done in the last problem, divide both sides by 20 to reduce the problem to:
.

.
The left side divides out to a quotient of 3 and the equation becomes:
.

.
On the right side apply Rule II (division) to split the term into two separate logarithms:
.
 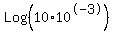
.
Notice that 10*10^-3 = 10^(-2). Substitute this into the right hand logarithm and get:
.
 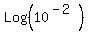
.
Apply Rule I (exponent rule) to 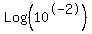 and get - and get - 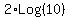 . But by Rule IV . But by Rule IV
you can see that Log base 10 of 10 = 1. (Think  which means y must be 1.) which means y must be 1.)
So - 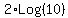 equals -2*1 equals -2. Substitute this result for equals -2*1 equals -2. Substitute this result for 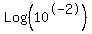
and the equation becomes:
.
 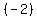
.
And this simplifies to 
.
Subtract 2 from both sides and the equation becomes:
.

.
Apply Rule IV to this equation and you get:
.

.
This agrees with the answer you had for this problem, but recall that 10 millivolts
was used in place of 10 microvolts to get the answer.
.
Hope this helps you get a handle on decibel equations.
|
|
|