SOLUTION: Good Day, Please help me solve exponential equation, express the solution set so that (a) solutions are in exact form and, if irrational (b) solutions are approximated to the ne

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Good Day, Please help me solve exponential equation, express the solution set so that (a) solutions are in exact form and, if irrational (b) solutions are approximated to the ne      Log On


   

Question 813780: Good Day,
Please help me solve exponential equation, express the solution set so that (a) solutions are in exact form and, if irrational (b) solutions are approximated to the nearest thousandth. support solution by using calculator 4^x-1 = 3^2x
Your help is greatly appreciated!
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
First, please post your questions in a relevant category. You posted this problem under Conic Sections but this problem has nothing to do with Conic Sections. You are more likely to get a fast response from a tutor if you post in a relevant category. (I've have changed the category of this problem to a relevant one.)

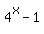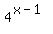Second, please put parentheses around exponents that are not just a number or a variable. I'm assuming that the left side is not 4%5Ex-1 as you posted it but 4%5E%28x-1%29. Clearly posted problems are also likely to get a fast response.

4%5E%28x-1%29+=+3%5E%282x%29
When the variable is in an exponent there are generally two ways to solve it:
  • With logarithms. This can always be done.
  • If the equation can be rewritten two equal exponentials (a base and an exponent) with equal bases, then the equation can be solved much more quickly (and without decimal approximations).
Your equation already has two equal exponentials. But the bases, 4 and 3, are not the same. Unless we can rewrite these with the same bases we will have to use logarithms. Since 4 is not a well-known power of 3 and 3 is not a well-known power of 4 and since 4 and 3 are not both well-known powers of some other number, we will have to use logarithms.

To solve this with logarithms we will find the logarithm of each side of our equation. But which base should we use for the logarithm? As it turns out, any base of logarithm may be used! But there are some advantages to choosing certain bases:
  • If you choose a base that matches the base of one of the exponentials, then the solution will end up being a simpler expression than if other bases are chosen.
  • If you choose a base your calculator "knows", like 10 or e, then the solution will be easily converted to a decimal approximation if one is wanted.
I will solve this equation twice, using both "smart" choices for bases.

Matching a base.
The equation has exponentials with bases of 4 and 3. We can choose either of these for the base of our logarithm. I will choose base 4:
log%284%2C+%284%5E%28x-1%29%29%29+=+log%284%2C+%283%5E%282x%29%29%29
Next we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, which allows us to "move" the exponent of the argument out in front of the log. (It is this very property that is the reason we use logarithms to solve these equations. They allow us to move the exponent, where the variable is, to a place (in front) where we can "get at it" with "regular" algebra.) Using this property on both sides we get:
%28x-1%29log%284%2C+%284%29%29+=+%282x%29log%284%2C+%283%29%29
And since log%284%2C+%284%29%29+=+1 be definition, this will simplify. (This is why matching the base of the log to the base of one of the exponentials results in simpler expressions.) So now we have:
x-1+=+%282x%29log%284%2C+%283%29%29
Now we solve for x. First we get the x terms on one side. Subtracting x from each side we get:
-1+=+%282x%29log%284%2C+%283%29%29+-+x
Factoring out x on the right side we get:
-1+=+%28x%29%282log%284%2C+%283%29%29+-+1%29
Dividing by 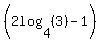%282log%284%2C+%283%29%29+-+1%29 we get:
%28-1%29%2F%282log%284%2C+%283%29%29+-+1%29+=+x
This is an exact expression for the solution to your equation. If now want a decimal approximation, then
  1. Use the base conversion formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29 to convert the base 4 log into an expression of base 10 or base e logs.
  2. Use your calculator on the converted expression.

Use a base your calculator "knows".
Most calculators "know" base 10 logs, "log", and base e logs, "ln". Either of these will work. I'll choose base e (aka natural logarithms). (Note: Since the logic behind each step below is exactly the same (with one exception), I will not explain these steps (except for the exception).)
4%5E%28x-1%29+=+3%5E%282x%29
ln%284%5E%28x-1%29%29+=+ln%283%5E%282x%29%29
%28x-1%29ln%284%29+=+%282x%29ln%283%29
This time the log on the left does not simplify like it did when we used base 4 logs. So we use the Distributive Property on the left side:
x%2Aln%284%29-ln%284%29+=+%282x%29ln%283%29
-ln%284%29+=+%282x%29ln%283%29-x%2Aln%284%29
-ln%284%29+=+x%282ln%283%29-ln%284%29%29
%28-ln%284%29%29%2F%282ln%283%29-ln%284%29%29+=+x
This is another exact expression for the solution to your equation (despite how different it looks from the one we found earlier.) This expression is not as simple (with 3 logs instead of 1) but it is easier to convert into a decimal approximation.

I'll leave it up to you and your calculator to find the decimal approximation for the answer. Hint: If you calculator has buttons for parentheses, as many do, then you can just type in 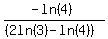%28-ln%284%29%29%2F%28%282ln%283%29-ln%284%29%29%29