SOLUTION: (X+1)(2+x )(3+x )(4+x)=120

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: (X+1)(2+x )(3+x )(4+x)=120      Log On


   

Question 813373: (X+1)(2+x )(3+x )(4+x)=120
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
%28x%2B1%29%282%2Bx+%29%283%2Bx+%29%284%2Bx%29=120
There's a clever, fast way to solve this and a slow, methodical way. First the fast way...

Notice two things:
  • If x is an integer, then x+1 would be the next integer, x+2 the integer after that, etc. So if x is an integer then the four factors on the left side of the equation would be four consecutive integers.
  • If you've worked with permutations much you may recognize 120 as 5! (read "five factorial"), which is 1*2*3*4*5. Since the 1 doesn't make a difference we could think of this as just 2*3*4*5... four consecutive integers.
Connecting these two we can see that if x+1 was 2 (or x = 1), then the equation would be true. The hardest part is remembering that there will be four consecutive odd integers (-2, -3, -4 and -5) which will also multiply to 120. For these the x would have to be -6 (so x+1 would be -5, x+2 would be -4, etc.). So by this reasoning we have two quick: 1 and -6. The other two solutions (there should be four because the highest exponent is 4) can be found using synthetic division to factor out (x-1) and (x-(-6)).

%28x%2B1%29%282%2Bx+%29%283%2Bx+%29%284%2Bx%29=120
The methodical approach would be to
  1. Multiply the left side out.
  2. Make the right side zero (by subtracting 120
  3. Try to factor what you have.
So we start by multiplying. Using FOIL on the first two factors and also on the last two factors we get:
%28x%5E2%2B3x%2B2%29%28x%5E2%2B7x%2B12%29=120
Multiplying the remaining factors:

which simplifies as follows:
x%5E4%2B7x%5E3%2B12x%5E2%2B3x%5E3%2B21x%5E2%2B36x%2B2x%5E2%2B14x%2B24=120
x%5E4%2B10x%5E3%2B35x%5E2%2B50x%2B24=120
Now we get a zero on the right:
x%5E4%2B10x%5E3%2B35x%5E2%2B50x-96=0
Now we try to factor. We will use trial and error of possible rational roots. Even though the leading coefficient of 1 has only one factor, the constant term of 96 has quite a few. So our list of possible rational roots is fairly long:
+1/1, +2/1, +3/1, +4/1, +6/1, +16/1, +24/1, +32/1, +48/1 and +96/1
which reduce to:
+1, +2, +3, +4, +6, +16, +24, +32, +48 and +96

It could take quite a while to find actual roots. But I'm going to be "brilliant" and "accidentally" choose the two roots we found in the fast solution: 1 and -6
1  |   1   10   35   50   -96
----        1   11   46    96
      ------------------------
       1   11   46   96     0
Surprise, surprise! Now we'll try -6 (using the other factor of "1 11 46 96" from the bottom row:
-6  |   1   11   46   96
-----       -6  -30  -96
       ------------------
        1    5   16    0
The "other" factor, "1 5 16", translates into x%5E2%2B5x%2B16. This is a quadratic which, if we cannot factor, we can use the quadratic formula to solve. x%5E2%2B5x%2B16 will not factor so on to the formula:
x+=+%28-%285%29+%2B-+sqrt%28%285%29%5E2-4%281%29%2816%29%29%29%2F2%281%29
which simplifies as follows:
x+=+%28-5+%2B-+sqrt%2825-64%29%29%2F2
x+=+%28-5+%2B-+sqrt%28-39%29%29%2F2
With the negative number in the square root, the other two solutions will be complex numbers. If you are only interested in real solutions then you can stop here. The only real solutions are 1 and -6. If you are interested in the complex solutions we continue:
x+=+%28-5+%2B-+sqrt%28-1%2A39%29%29%2F2
x+=+%28-5+%2B-+sqrt%28-1%29%2Asqrt%2839%29%29%2F2
x+=+%28-5+%2B-+i%2Asqrt%2839%29%29%2F2
which is short for:
x+=+%28-5+%2B+i%2Asqrt%2839%29%29%2F2 or x+=+%28-5+-+i%2Asqrt%2839%29%29%2F2
In standard a + bi form for complex numbers, these would be:
x+=+%28-5%29%2F2+%2B+%28sqrt%2839%29%2F2%29%2Ai or x+=+%28-5%29%2F2+%2B+%28-sqrt%2839%29%2F2%29%2Ai

Making the four roots: 1, -6, 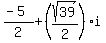%28-5%29%2F2+%2B+%28sqrt%2839%29%2F2%29%2Ai, %28-5%29%2F2+%2B+%28-sqrt%2839%29%2F2%29%2Ai