(1/log2)-(1/log 3)+(1/log4)-..... what will be the nth term?
The nth term is 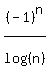 for n = 2,3,4,...
or
the nth term will be
for n = 2,3,4,...
or
the nth term will be 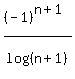 for n = 1,2,3,...
or
the nth term will be
for n = 1,2,3,...
or
the nth term will be  for n = 0,1,2,...
It depends on what value you want to start the dummy variable n.
----
whether it is right to write the series from n=2 to infinity (1/log n)
It is OK if you include the sign-alternating factor (-1)n, but not
if you don't include it.
S =
for n = 0,1,2,...
It depends on what value you want to start the dummy variable n.
----
whether it is right to write the series from n=2 to infinity (1/log n)
It is OK if you include the sign-alternating factor (-1)n, but not
if you don't include it.
S =  is OK
An alternating series converges (at least conditionally) if the
nth term approaches 0.
Edwin
is OK
An alternating series converges (at least conditionally) if the
nth term approaches 0.
Edwin