|
Question 813301: Use the rational root theorem to find all rational roots of the function. Then find all actual roots.
3x^3+x^2-15x-5
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 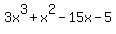
The possible rational roots of a polynomial are all the ratios, positive and negative, that can be formed using a factor of the constant term in the numerator and a factor of the leading coefficient in the denominator.
Your constant term is 5. (Actually it is -5 but since we will be using all positive and negative ratios it doesn't make any difference if we use 5 or -5.) The factors of 5 are just 1 and 5.
Your leading coefficient is 3 whose factors are just 1 and 3.
Forming the ratios (as described above) we get the following list of possible rational roots:
+1/1, +5/1, +1/3 and +5/3.
The first two simplify:
+1, +5, +1/3 and +5/3.
Now we see which of these, if any, are actual roots. We'll use synthetic division to check. Checking 1:
1 | 3 1 -15 -5
---- 3 4 -11
------------------
3 4 -11 -16
The remainder is the -16 in the lower right corner. Since it is not zero 1 is not a root. Checking x = -1:
-1 | 3 1 -15 -5
---- -3 2 13
------------------
3 -2 -13 8
The remainder is the 8. So -1 is not a root, either. But since this remainder is positive and the one we got for 1 was negative, there is a root somewhere in between. Since 8 is closer to zero than -16 I'm guessing that the root is closer to -1 than to 1. So I will try -1/3 next:
-1/3 | 3 1 -15 -5
------ -1 0 5
------------------
3 0 -15 0
And we have a winner! -1/3 is a root (and 3x+1 is a factor). Not only that, but the rest of the bottom row tells us the other factor. The "3 0 -15" translates into 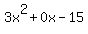 or simply or simply 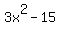 . Since this is a quadratic we can find the remaining roots without having to try more rational roots. All we have to do is solve: . Since this is a quadratic we can find the remaining roots without having to try more rational roots. All we have to do is solve:

Adding 15:

Dividing by 3:

Square root of each side:

(Note: The zero is there only because algebra.com's formula drawing software will not let me use the "plus or minus" symbol without a number in front.)
So the three roots are -1/3 (rational),  (irrational) and (irrational) and  (irrational) (irrational)
|
|
|
| |