SOLUTION: The vertex and focus of the parabola y^2-4x+20=0 are one focus and one vertex respectively of an ellipse whose center is the origin. Find the equation of the ellipse

y²-4x+20 = 0  (y is squared so it is a parabola 
               with horizontal axis of symmetry)

      y² = 4x-20

  (y-0)² = 4(x-5)

Compare to

  (y-k)² = 4p(x-h), with vertex (h,k),

so vertex = (5,0)

and since 4p=4, p=1 so distance from
vertex to focus is |p| = 1.

p is positive so it opens to the right.

The graph of the parabola is 



So the focus is |p|=1 unit to the right 
of the vertex, or (6,0).

Now we want the equation of an ellipse with center (0,0)
focus (5,0), and vertex (6,0), like this green ellipse:



In an ellipse the distance from center to vertex is "a",
the semi-major axis, and the distance from (0,0) to (6,0) is a=6.
The distance from center to focus is "c", and the distance from 
(0,0,) to (5,0) is c=5.  The Pythagorean relationship for all 
ellipses is

c² = a²-b² where "b" is the semi-minor axis. So
5² = 6²-b²
25 = 36-b²
b² = 36-25
b² = 11
 b = √11 

This ellipse has horizontal major axis, and its equation is

  1
 
  1
 
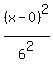
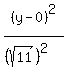
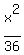
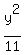
  1

Edwin