SOLUTION: Working together gene and robert can mow the lawn in 2 hours. When Gene works alone it takes him 3 hours longer than it takes robert when he works alone. How long does it take robe

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Working together gene and robert can mow the lawn in 2 hours. When Gene works alone it takes him 3 hours longer than it takes robert when he works alone. How long does it take robe      Log On


   

Question 812216: Working together gene and robert can mow the lawn in 2 hours. When Gene works alone it takes him 3 hours longer than it takes robert when he works alone. How long does it take robert to mow the lawn by himself.
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
How long does it take robert to mow the lawn by himself?
Let x = the number of hours it takes Robert to mow the lawn by himself.

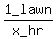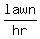So Robert's mowing rate is 1 lawn per x hours or 1_lawn%2Fx_hr or 1%2Fxlawn%2Fhr.

When Gene works alone it takes him 3 hours longer than it takes robert when he works alone.
Then the number of hours it takes Gene to mow the lawn by himself = x+3

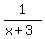
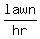So Gene's mowing rate is 1 lawn per x+3 hours or 1_lawn%2Fx%2B3_hr or 1%2F%28x%2B3%29lawn%2Fhr.

Working together gene and robert can mow the lawn in 2 hours.
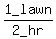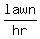So their combined working rate is 1 lawn per 2 hours or 1_lawn%2F2_hr or 1%2F2lawn%2Fhr.

The equation comes from 

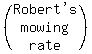
    %28matrix%283%2C1%2C%22Robert%27s%22%2Cmowing%2Crate%29%29%22%22%2B%22%22%28matrix%283%2C1%2C%22Gene%27s%22%2Cmowing%2Crate%29%29 %22%22=%22%22 %28matrix%284%2C1%2CTheir%2Ccombined%2Cmowing%2Crate%29%29

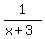
             1%2Fx%22%22%2B%22%221%2F%28x%2B3%29 %22%22=%22%22 1%2F2

Multiply through by LCD = 2x(x+3)

Answer: x = 3 hours. 

Edwin