Question 812096: Please help me solve this word problem: a rectangular space of 252 square feet is allocated for living and dining areas in a house. Find the width of the square living area given that the width of the dining area is 9 feet.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! It would not make sense for the total rectangular area to be 9 feet wide, wide a very small 9 foot by 9 foot living room on one end, and a very long 9-foot wide dining area attached, like this:
 That would be an easy answer, but a ridiculous floor plan. That would be an easy answer, but a ridiculous floor plan.
What they have in mind looks like this:
 The living area is a square with sides measuring The living area is a square with sides measuring  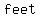 . The dining room measures . The dining room measures  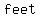 by 9 feet. by 9 feet.
The total combined living plus dining area is a rectangle measuring  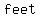 by by 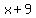 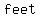 . .
So  is your starting equation. is your starting equation.
You want to find  . .
From there on, I would suggest factoring. It gets you from here to the answer in a few short steps.
If you cannot or will not do factoring, you can transform that equation into a more familiar form, and solve it without factoring.
 --> --> --> -->
Then you could solve by completing the square, or apply the quadratic formula.
I'll show you both ways further down.
In the meantime, I will try to convince you that factoring often makes math easier.
The factoring required for this problem is easy, but it is good practice because, in math, factoring never completely goes away. It keeps coming back. When you are done with the math chapter on polynomials and factoring, you may think that you can forget it. (I did). Forget that idea. The need for factoring will keep coming up, over, and over, for as long as you have a math class.
Back to the problem.
The starting equation,  says that there are two numbers, says that there are two numbers,  and and 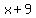 , that area , that area  units apart, and multiply to give units apart, and multiply to give 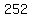 . .
What are the factors of 252? You can tell that it is even, so  is a factor. You may even realize that it is a multiple of is a factor. You may even realize that it is a multiple of  because because  is a multiple of is a multiple of  . .
You realize that it is a multiple of  and and  because the digits add up to because the digits add up to  . .
If you divide 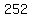 by by  , or divide by , or divide by  twice , you get twice , you get  , so that tells you that , so that tells you that  is also a factor, and that is also a factor, and that
 . .
However, you do not need to figure out all that to solve the problem. You just need two numbers, differing by 9, whose product is 252.
You can start trying numbers in order.




5 is not a factor but 252 divided by 6 is 42, so

So far the pairs of factors differ in a lot more than 9,
 but the differences are getting smaller. but the differences are getting smaller.
7 and 8 do not evenly divide 252, but 9 does, and

10 and 11 do not work, but 252 divides by 12 to give 21, so
 and and  so we have found the two factors so we have found the two factors
 and and  are the width and length of the whole rectangle, and the living area is a square with sides measuring are the width and length of the whole rectangle, and the living area is a square with sides measuring  . .
Solving the quadratic equation by completing the square:
If a quadratic equation has solutions that are rational numbers, it is easy enough to solve it by factoring (although not always as easy as done above).
Otherwise you can do it without formulas by "completing the square."
Starting from  , you could realize that the left side of that equation is part of , you could realize that the left side of that equation is part of
 , ,
so adding 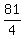 to both sides of the equal sign in to both sides of the equal sign in  you get you get




So either  --> --> --> --> --> --> , ,
or  --> --> --> --> --> --> , which does not make sense as a room length because it is a negative number. , which does not make sense as a room length because it is a negative number.
Solving the quadratic equation by using the quadratic formula:
A quadratic equation of the form  , ,
if it has any real solutions, the solutions are given by

That applies to  , where , where
 , ,  , and , and  . .
So 


 --> --> 
Since  cannot be the measurement of the side of the living area in feet, the only solution that makes sense, so cannot be the measurement of the side of the living area in feet, the only solution that makes sense, so  and the living area is a square with sides measuring and the living area is a square with sides measuring  . .
|
|
|