SOLUTION: y=9-x^2. Find vertex and graph.

Algebra ->  Graphs -> SOLUTION: y=9-x^2. Find vertex and graph.      Log On


   

Question 81200: y=9-x^2. Find vertex and graph.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Completing the Square to Get a Quadratic into Vertex Form


y=-1+x%5E2%2B0+x%2B9 Start with the given equation



y-9=-1+x%5E2%2B0+x Subtract 9 from both sides



y-9=-1%28x%5E2%2B%280%29x%29 Factor out the leading coefficient -1



Take half of the x coefficient 0 to get 0 (ie %281%2F2%29%280%29=0).


Now square 0 to get 0 (ie %280%29%5E2=%280%29%280%29=0)





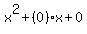y-9=-1%28x%5E2%2B%280%29x%2B0-0%29 Now add and subtract this value inside the parenthesis. Doing both the addition and subtraction of 0 does not change the equation




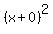
y-9=-1%28%28x%2B0%29%5E2-0%29 Now factor x%5E2%2B%280%29x%2B0 to get %28x%2B0%29%5E2



y-9=-1%28x%2B0%29%5E2%2B1%280%29 Distribute



y-9=-1%28x%2B0%29%5E2-0 Multiply



y=-1%28x%2B0%29%5E2-0%2B9 Now add 9 to both sides to isolate y



y=-1%28x%2B0%29%5E2%2B9 Combine like terms




Now the quadratic is in vertex form y=a%28x-h%29%5E2%2Bk where a=-1, h=-0, and k=9. Remember (h,k) is the vertex and "a" is the stretch/compression factor.




Check:


Notice if we graph the original equation y=-1x%5E2%2B0x%2B9 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C-1x%5E2%2B0x%2B9%29 Graph of y=-1x%5E2%2B0x%2B9. Notice how the vertex is (-0,9).



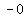Notice if we graph the final equation y=-1%28x%2B0%29%5E2%2B9 we get:


graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C-1%28x%2B0%29%5E2%2B9%29 Graph of y=-1%28x%2B0%29%5E2%2B9. Notice how the vertex is also (-0,9).



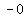So if these two equations were graphed on the same coordinate plane, one would overlap another perfectly. So this visually verifies our answer.