Question 810983: Good day, I would like help with finding the intervals of increase and decrease of this function and its local minimum and maximum if it has them. Since it is a rational function I used the quotient rule to derive it but I don't think I'm getting it right. It is y = x/(x-1)^2.
Thank you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I see two ways to calculate the derivative, and I like that,
because I know I make mistakes, so if both answers agree I'm reassured,
and if they don not agree, I try to find and fix errors.
(I will not say how it went this time).
This is what I ended up with:
Using the quotient rule

The other way:
 . .
So  is another expression for the function, is another expression for the function,
and it could be useful for derivative calculation and more.
Now I will calculate the derivative of 

With both answers in agreement, now I am pretty sure that
 is the derivative. is the derivative.
 changes sign at changes sign at  and at and at  . .
For  , where , where  , ,
 so so 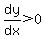 and the function is increasing at that point, and the function is increasing at that point,
and at all points with 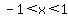 . .
The denominator of  changes sign at changes sign at  , ,
which we know is a vertical asymptote,
so  changes sign at changes sign at  . .
For 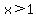 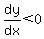 and the function starts decreasing after and the function starts decreasing after  , (but the function does not change sign there). , (but the function does not change sign there).
The numerator of  changes sign at changes sign at  , ,
so for  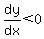 and the function is decreasing. and the function is decreasing.
Since the function decreases for  , ,
increases for 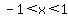 , ,
and for  the function exists, with the function exists, with  , ,
the function has a local minimum at  . .
 , and zooming in , and zooming in 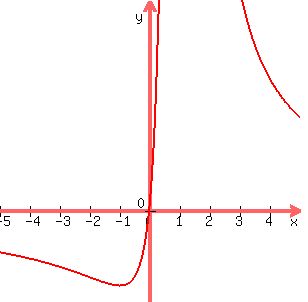
|
|
|