Question 810620: An observer on the roof of building A measures a 26° angle of depression between the horizontal and the base of building B. The angle of elevation from the same point to the roof of the second building is 41.34°. What is the height of building B if the height of building A is 150 ft? Assume buildings A and B are on the same horizontal plane. (Round your answer to two decimal places.)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The sketch below shows the two buildings as green buildings rectangles.
  
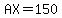
From the right triangles below horizontal line AH (triangles AHY and AXY) we know that
  --> 
If we want to solve the problem in 3 steps,
with that we can calculate an approximate value for  = approximately  ,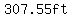
and then we use that value and right triangle ABH to find the distance BH,
which we add to  to find 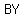 , the height of the tall building.
If we want to be fancy, and do all of the calculations in one fancy formula,
we keep working with variables on right triangle ABH.
Then,
That is the exact value answer that a mathematician would give.
A physics professor would tell you to consider the uncertainty in the measurements
(of the height of the shorter building, and the angles),
and may give an answer such as  .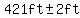
A more practical engineer, calculates the approximate value as
 or more likely  .
I suspect that a high school math teacher would like as an answer too.
|
|
|
