Question 809615: Please help me with this Calculus II question:
Find all points of intersection of the given curves. (Assume
0 ≤ θ ≤ 2π.
Order your answers from smallest to largest θ. If an intersection occurs at the pole, enter POLE in the first answer blank.)
r = 1 − cos θ, r = 1 + sin θ
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me with this Calculus II question:
Find all points of intersection of the given curves. (Assume
0 ≤ θ ≤ 2π.
Order your answers from smallest to largest θ. If an intersection occurs at the pole, enter POLE in the first answer blank.)
r = 1 − cos θ, r = 1 + sin θ
1 − cos θ = 1 + sin θ , since both = r
−cos θ = sin θ
Divide both sides by cos θ
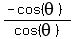 = = 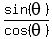 -1 = tan(θ)
So θ has two possible values where 0 ≤ θ ≤ 2π. the tangent is negative
in Q2 and Q4 and the reference angle is 45° or
-1 = tan(θ)
So θ has two possible values where 0 ≤ θ ≤ 2π. the tangent is negative
in Q2 and Q4 and the reference angle is 45° or  , so θ is , so θ is  in Q2 or
in Q2 or  in Q4.
So the smaller value of θ is in Q4.
So the smaller value of θ is  , and the value of r is gotten
by substituting , and the value of r is gotten
by substituting  for θ in either of the original equations:
r = 1 − cos θ = 1 - cos for θ in either of the original equations:
r = 1 − cos θ = 1 - cos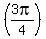 = 1 - = 1 - 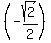 = 1 + = 1 +  = =  So the first point is (r,θ) = (
So the first point is (r,θ) = ( , ,  )
The larger value of θ is )
The larger value of θ is  , and the value of r is gotten
by substituting , and the value of r is gotten
by substituting  for θ in either of the original equations:
r = 1 − cos θ = 1 - cos for θ in either of the original equations:
r = 1 − cos θ = 1 - cos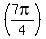 = 1 - = 1 - 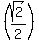 = 1 - = 1 -  = =  So the second point is (r,θ) = (
So the second point is (r,θ) = ( , ,  )
Edwin )
Edwin
|
|
|